.
Find the values of m for which the equation 
A) has exactly 2  solutions
solutions
B) has exactly 1  solution
solution
C) has exactly 0  solutions
solutions
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
It is about the discriminant of the quadratic equation.
The discriminant in this case is d = b^2 - 4ac, where
a = 1, b = (m-2), and c = 4.
So, d = (m-2)^2 - 4*4 = 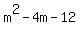 .
A) The equation
.
A) The equation  =
=  has exactly 2 real solutions if and only if d > 0.
It is equivalent to an inequality
has exactly 2 real solutions if and only if d > 0.
It is equivalent to an inequality 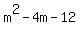 >
>  , which has the solutions m < -2 and/or m > 6.
B) The equation
, which has the solutions m < -2 and/or m > 6.
B) The equation  =
=  has exactly 1 real solutions if and only if d = 0.
It is equivalent to an equation
has exactly 1 real solutions if and only if d = 0.
It is equivalent to an equation 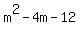 =
=  , which has two solutions m = 6 and/or m = -2.
C) The equation
, which has two solutions m = 6 and/or m = -2.
C) The equation  =
=  has exactly 0 real solutions if and only if d < 0.
It is equivalent to an inequality
has exactly 0 real solutions if and only if d < 0.
It is equivalent to an inequality 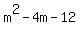 <
<  , which has the solutions -2 < m < 6.
Answer. A) has exactly 2 real solutions if and only if m < -2 and/or m > 6.
B) has exactly 1 real solution if and only if m = -2 and/or m = 6.
C) has exactly 0 real solutions if and only if -2 < m < 6.
, which has the solutions -2 < m < 6.
Answer. A) has exactly 2 real solutions if and only if m < -2 and/or m > 6.
B) has exactly 1 real solution if and only if m = -2 and/or m = 6.
C) has exactly 0 real solutions if and only if -2 < m < 6.