SOLUTION: With reference to the fact that the functions log2 x and 2^x undo each other, explain each of the following statements. (a) log2 0 is undefined. (b) log2 x is negative when x i

Algebra ->  Equations -> SOLUTION: With reference to the fact that the functions log2 x and 2^x undo each other, explain each of the following statements. (a) log2 0 is undefined. (b) log2 x is negative when x i      Log On


   

Question 1032364: With reference to the fact that the functions log2 x and 2^x undo each other, explain each of the
following statements.
(a) log2 0 is undefined.
(b) log2 x is negative when x is between 0 and 1.
(c) log2 500 is between 8 and 9.
(d) An x can be found so that log2(x) is greater than 1, 000, 000.
in all the log2 above 2 is the power of the log . I couldn't find a way to put the correct form in here.
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
(a) 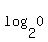log%282%2C0%29 is undefined because there is NO real number x such that 2%5Ex+=+0.
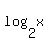(b) +log%282%2C+x%29 is negative when x is between 0 and 1 because, if you will notice the graph of y=2%5Ex, for 0+%3C+y=2%5Ex+%3C1, the corresponding set of pullback x-values is exactly the interval (-infinity, 0).
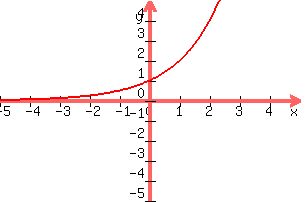
graph%28+300%2C+200%2C+-5%2C+5%2C+-5%2C+5%2C+2%5Ex%29
(c) This is easy, because 2%5E8+=256+%3C+500+%3C+2%5E9=512.
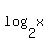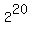(d) An x can be found so that log%282%2Cx%29 is greater than 1,000,000. Indeed, 2%5E20+ = 1,048,576 > 1,000,000.
You have to remember that logarithm is just a fancy way of writing an exponent satisfying a base condition.