Question 1026750: find the equation of a line , if the line passes through (2,2) and the y-int. is twice the x-int.
Found 2 solutions by Theo, MathTherapy:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! slope intercept form of the equation for a straight line is y = mx + b.
m is the slope.
b is the y-intercept.
since the line passes through the point (2,2), you can replace y with 2 and x with 2 to get:
2 = 2m + b
since b = 2m, you can replace b with 2m to get:
2 = 2m + 2m
combine line terms to get 2 = 4m.
divide both sides by 4 to get 2/4 = m.
simplify to get m = 1/2.
since b = 2m, then b = 1.
your equation is y = 1/2 * x + 1.
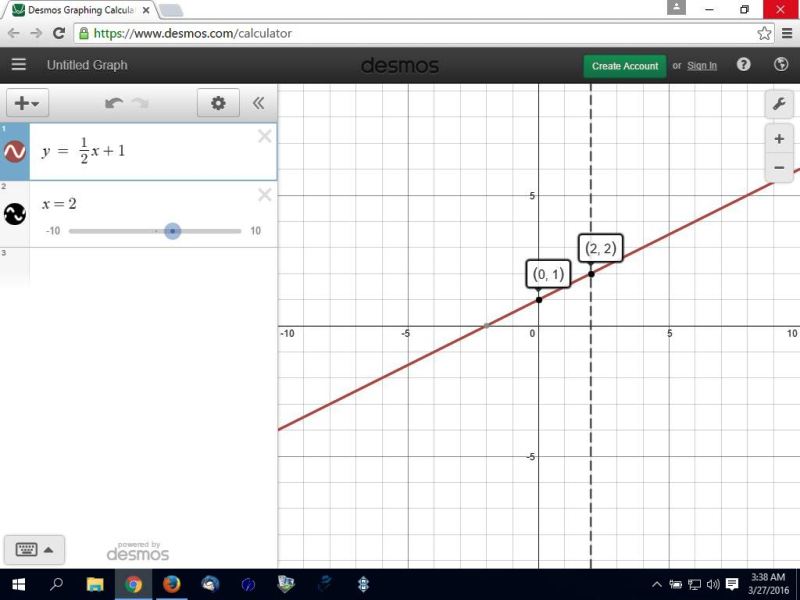
here's a graph of your equation.
you can see that the line passes through the point (2,2 and has a y-intercept of 1.
you can also see that the slope is 1/2 by taking the 2 points indicated and solving for the slope.
one of the points is (2,2) and the other point is (0,1).
y2 = (2,2)
y1 = (0,1)
y2-y1 = 1
x2-x1 = 2
slope is equal to (y2-y1) / (x2-x1) = 1/2.
Answer by MathTherapy(10551)  (Show Source):
|
|
|
