SOLUTION: "Find the value(s) of k so that the graph of the equation y= |x + k| - 2 has an x-intercept of 4." I can't remember how to do this kind of problem, and my 20-year-old algebra textb

y = |x + k| - 2

"has an x-intercept of 4." means that the graph passes through
the point (4,0),  Since 4 is the x-coordinate and 0 is the 
y-coordinate, substitute x=4 and y=0

0 = |4 + k| - 2

Add 2 to both sides

2 = |4 + k|

Break into two equations:

4 + k = 2   and   4 + k = -2
    k = -2            k = -6

So the two values of k means that there are two
answers:

y = |x - 2| - 2     and   y = |x - 6| - 2

Here are the two graphs:



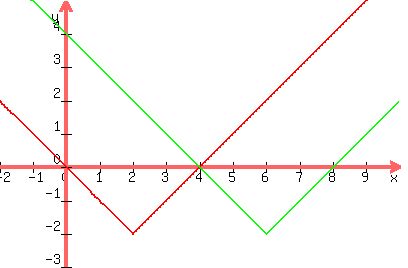Notice that they both go through the point (4,0) on the
x axis.  They both intercept the x-axis there.

Edwin