Question 1014361: 3x²-31x-60=0 plz explain me in detail
Found 2 solutions by KMST, Edwin McCravy:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  is a quadratic equation. is a quadratic equation.
That means that it can be written (in this case, it is written)
as a degree 2 polynomial equal to zero.
In simpler words,  appears squared as appears squared as  in the equation; in the equation;
it may also appear as  , maybe multiplied by a number, , maybe multiplied by a number,
and there is no other strange business with 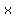 , no , no  in a denominator, no in a denominator, no  , no , no 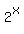 , etc). , etc).
There are 3 possible methods to solve a quadratic equation:
factoring (which only works if there are rational solutions),
"completing the square", and
using the quadratic formula.
In this case, I would use the quadratic formula.
The quadratic formula says that the solutions to an equation of the form
 , if they exist in the math class you are taking, , if they exist in the math class you are taking,
are given by 
For  <--> <--> , ,
 , ,  , and , and  , so , so




That gives you two solutions that exist,
because the square root of a positive number exists for most math class levels.
In some cases those square roots are irrational numbers, such as  , ,
but in this case  turned out to be a nice whole number. turned out to be a nice whole number.
So,  <--> <--> gives us two solutions gives us two solutions
 . .
THE FACTORING WAY TO SOLVE IT
consists of figuring out that 
and re-writing  as as  . .
If  , one of those two bracketed factors must be zero, so , one of those two bracketed factors must be zero, so
 ---> ---> ---> ---> . .
Figuring out that  requires some thinking, requires some thinking,
but you do not have to mess with the quadratic formula.
To begin, you multiply the coefficient of  and the independent term (the one without and the independent term (the one without  ); );
 . .
Then you look for pairs of factors of that number
that add up to the coefficient of  in your equation: in your equation:  . .
You look for pairs of factors of  , and worry about the minus sign later. , and worry about the minus sign later.
Sometimes there is a lot of pairs, and you have to organize.
I like to look for the smaller factor starting with  , ,
and then see if I can make factor pairs where the smaller factor is  , ,  , ,  , etc, in that order. , etc, in that order.






 and and  are not factors of are not factors of 


 is not a factor of 180 is not a factor of 180

 and and  are not factors of are not factors of 
and factors equal to  and larger have already been found. and larger have already been found.
From the list above, we know that
 and and  are factor pairs that multiply to yield are factor pairs that multiply to yield 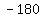 , ,
but you want them to add up to  . .
The sum  has the wrong sign. has the wrong sign.
 has the expected negative sign, and is close to has the expected negative sign, and is close to  . .
Obviously we want to give the minus sign to the larger factor, to make the sum negative.
You also see that  and and  are a little to far apart, are a little to far apart,
and that makes the difference  larger than larger than 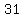 . .
So we try a pair of factors that are a little closer together:
 and and  , ,
and discover that we have found our pair of factors.
Now, you re-write 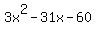 using those factors, like this: using those factors, like this:
 . .
Finally, find common factors, and "take out the common factors", twice:

Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since the leading coefficient 3
can only be factored only one way,
I think the trial-and-error factoring
method is better in this case:
3x²-31x-60=0
Since the last term -60 is negative,
we know that the absolute value
of the middle coefficient, -31, which
is 31, must be the result when the
absolute values of the product of the
outer and inner terms are subtracted.
[If the last term were +, we would
know that they would be added].
The factorizations are either of
these forms:
(x A)(3x B)
(x B)(3x A)
where A and B are as in this chart:
∥ A, B ∥ |B-3A|,|A-3B|
∥ 1,60 ∥ 57 179
∥ 2,30 ∥ 24 88
∥ 3,20 ∥ 11 57
∥ 4,15 ∥ 3 41
∥ 5,12 ∥ 3 31
∥ 6,10 ∥ 8 24
How to make that chart:
In the first column we list all the
factor pairs of 60. Then we form
the differences mentally, until we
come to the absolute value of the
coefficient of the middle term, 31.
In this case it was the red one.
Often when using this method, we will
reach it much sooner, and stop
whenever we reach it.
Now since the 31 came from the second
column we know that the factorization
is of the form:
(x B)(3x A)
so the factorization is
(x 12)(3x 5)
Now the product of the outer terms
is 5x and the product of the inner
terms is 36x, so to get the middle
term -31x, the 36x must be made
negative and the 5x must be made
positive. So the factorization is
(x-12)(3x+5).
It takes some practice to use this
method, but it'll save time when
either the first or last term can
be factored only one way.
Edwin
|
|
|