Someone help please, it says.
Use synthetic division to solve : x^5-4x^4-2x^3+4x^2+x=0
Show work please. Thanks

 --- Factoring out GCF, x
--- Factoring out GCF, x
 -------- Factoring out GCF, x
Using the RATIONAL ROOT THEOREM we find that 2 roots are:
-------- Factoring out GCF, x
Using the RATIONAL ROOT THEOREM we find that 2 roots are: 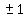 Use synthetic division with a divisor/root of 1
1 | 1 - 4 - 2 + 4 + 1
| + 1 - 3 - 5 - 1
--------------------------
1 - 3 - 5 - 1 0
Use synthetic division with a divisor/root of 1
1 | 1 - 4 - 2 + 4 + 1
| + 1 - 3 - 5 - 1
--------------------------
1 - 3 - 5 - 1 0
Now we have: 
Use synthetic division with a divisor/root of - 1
- 1 | 1 - 3 - 5 - 1
| - 1 + 4 + 1
----------------------
1 - 4 - 1 0
Now we have: 
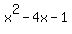 does not have any INTEGER roots, so you can use the following to get the final 2 roots:
1) the quadratic equation
2) completing the square
3) graphing
does not have any INTEGER roots, so you can use the following to get the final 2 roots:
1) the quadratic equation
2) completing the square
3) graphing