SOLUTION: Find the equation of the line a) parallel b) perpendicular to 2x-3y=6 and passing at a distance 2sqrt (3) units from (-1,2)

Algebra ->  Equations -> SOLUTION: Find the equation of the line a) parallel b) perpendicular to 2x-3y=6 and passing at a distance 2sqrt (3) units from (-1,2)      Log On


   

Question 1009850: Find the equation of the line a) parallel b) perpendicular to 2x-3y=6 and passing at a distance 2sqrt (3) units from (-1,2)
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
THE EXPECTED WAY TO SOLVE IT:
You were taught the the distance from a point P%28x%5B0%5D%2Cy%5B0%5D%29
to a line ax%2Bby%2Bc=0 is measured along segment PQ ,
from P to the closest point on the line, point Q .
They also taught you a formula to find that distance:
,
and maybe even formulas to find the coordinates of point Q .
a) Lines parallel to 2x-3y=6<-->2x-3y-6=0
Have the equation 2x-3y%2Bc=0 .
Blindly applying that formula,

d%282x-3y%2Bc=0%2CP%28-1%2C2%29%29=abs%28-2-6%2Bc%29%2Fsqrt%284%2B9%29
d%282x-3y%2Bc=0%2CP%28-1%2C2%29%29=abs%28c-8%29%2Fsqrt%2813%29 .
And since we know that distance must be 2sqrt%283%29 ,
abs%28c-8%29%2Fsqrt%2813%29=2sqrt%283%29-->abs%28c-8%29=2sqrt%283%29%2Asqrt%2813%29-->abs%28c-8%29=2sqrt%2839%29-->c=8+%2B-+2sqrt%2839%29 .
So the equation of the two lines parallel to 2x-3y=6 ,
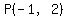and passing at a distance 2sqrt%283%29 units from P%28-1%2C2%29 , is
highlight%282x-3y%2B8+%2B-+3sqrt%2839%29=0%29
b) Line 2x-3y=6<-->2x-6=3y<-->y=%282%2F3%29x-6%2F3<-->y=%282%2F3%29x-2
has a slope of 2%2F3 .
Lines perpendicular to 2x-3y=6 have a slope of
%28-1%29%2F%282%2F3%29=%28-1%29%2A%283%2F2%29=-3%2F2 .
Their equation will be
y=-%283%2F2%29x%2Bb<-->2y=-3x%2B2b<-->3x%2B2y-2b=0 ,
which we could write as 3x%2B2y%2Bc=0.
As before

d%283x%2B2y%2Bc=0%2CP%28-1%2C2%29%29=abs%28-3%2B4%2Bc%29%2Fsqrt%289%2B4%29
d%283x%2B2y%2Bc=0%2CP%28-1%2C2%29%29=abs%28c%2B1%29%2Fsqrt%2813%29 ,
and since that distance must be 2sqrt%283%29 ,
abs%28c%2B1%29%2Fsqrt%2813%29=2sqrt%283%29-->abs%28c%2B1%29=2sqrt%283%29%2Asqrt%2813%29-->abs%28c%2B1%29=2sqrt%2839%29-->c=-1+%2B-+2sqrt%2839%29 .
So the equation of the two lines perpendicular to 2x-3y=6 ,
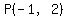and passing at a distance 2sqrt%283%29 units from P%28-1%2C2%29 , is
highlight%283x%2B2y-1+%2B-+3sqrt%2839%29=0%29 .

THE PICTURES AND EXPLANATION FOR THE SITUATION:
The line represented by 2x-3y=6 and
the circle that is the locus of all the points 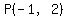2sqrt%283%29 units from P%28-1%2C2%29
are shown below.
The circle is centered at p and has a radius of 2sqrt%283%29 units.The equation for the circle is %28x%2B1%29%5E2%2B%28y-2%29%5E2=%282sqrt%283%29%29%5E2<-->%28x%2B1%29%5E2%2B%28y-2%29%5E2=12 .
There is more than one line
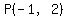parallel to 2x-3y=6 and passing at a distance 2sqrt%283%29 units from P%28-1%2C2%29 ,
and there is more than one line
perpendicular to 2x-3y=6 and passing at a distance 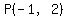2sqrt%283%29 units from P%28-1%2C2%29 .
The way I read/interpret the problem, we want lines a) parallel, and b) perpendicular to 2x-3y=6 , and tangent to the circle %28x%2B1%29%5E2%2B%28y-2%29%5E2=12 .
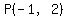Only 1 point of each of those lines is at a distance 2sqrt%283%29 units from P%28-1%2C2%29 .
That point is the intersection of the line with the circle %28x%2B1%29%5E2%2B%28y-2%29%5E2=12 .
The remaining point on each of the lines is at a distance greater than 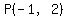2sqrt%283%29 units from P%28-1%2C2%29 ,
and therefore is outside the circle of radius.

There are two lines parallel to 2x-3y=6 ,
and tangent to the circle %28x%2B1%29%5E2%2B%28y-2%29%5E2=12 .
They are tangent at points Q and R .
There are two lines perpendicular to 2x-3y=6 ,
and tangent to the circle %28x%2B1%29%5E2%2B%28y-2%29%5E2=12 .
They are tangent at points S and T .
Each of those lines is perpendicular to the radius at the point of tangency.
So PQ and PR are perpendicular to the two lines parallel to 2x-3y=6 and must be perpendicular to 2x-3y=6 itself.
and PS and PT are perpendicular to the two lines perpendicular to 2x-3y=6 and must be parallel to 2x-3y=6 .