Question 800889: A student found that all three digit numbers of the form abc, where a+b is a multiple of 7, are divisible by 7. She would like to know why. Give an algebraic expression.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! That student was wrong, and a single counterexample can prove her wrong.
770 is a 3 digit number that is a multiple of 7, and its first two digits add up to 14, which is a multiple of 7.
However, 771, 772, 773, 774, 775, 776, 778, and 779, with the same two first digits are not multiples of 7.
I propose a different divisibility by 7 rule.
All three digit numbers of the form aba, where a+b is a multiple of 7, are divisible by 7.
The value of a three digit numbers of the form aba is
If 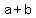 is a multiple of 7, either  or  .
Splitting the proof into two cases makes it easier to see and write.
(Otherwise I have to write that  where  is an integer).
If , then  , and substituting we find the value of aba to be
Since  is a digit,  is an integer, and so is  .
Then  divides evenly by 7 and the quotient is .
If , then  , and substituting we find the value of aba to be
Since is a digit, is an integer, and so is  .
Then  divides evenly by 7 and the quotient is .
|
|
|
