Question 611475: i am a factor of 120, and a common multiple of 3, 4, and 10. The sum of my digits is 6.
Answer by KMST(5330)   (Show Source): (Show Source):
You can put this solution on YOUR website! 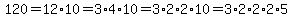
So, the prime factorization of 120 is

while  and and 
A multiple of 4 needs to have 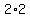 in its factorization. in its factorization.
A multiple of 10 needs to have  in its factorization. in its factorization.
A multiple of 3 needs to have  in its factorization. in its factorization.
The number  is the smallest number that has all the factors needed, and is the answer to the problem. is the smallest number that has all the factors needed, and is the answer to the problem.
 so it is a multiple of 10. so it is a multiple of 10.
 so it is a multiple of 3. so it is a multiple of 3.
 so it is a multiple of 4. so it is a multiple of 4.
We could include more factors, but that would result in larger numbers, and most of them would be larger than 120, so they would not be factors of 120, and would not be a solution to the problem.
Adding factors, the smallest number we could get is when we include the smallest factor (another 2) as an extra factor. Then we get the only other factor of 120 that is also a common multiple of 3, 4, and 10.
 , is a multiple of 120, but its digits do not add to 6. , is a multiple of 120, but its digits do not add to 6.
|
|
|