Question 1208953: Suppose a >= 2 and n is a natural number larger than 1.
How can I prove that if n is odd, then a^n+1 is not prime?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3827)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It wasn't stated, but I'm assuming 'a' is an integer.
I'll also assume the +1 is not in the exponent.
If the +1 was in the exponent, then it's very easy to show that a^(n+1) is always composite regardless if n was even or odd.
To factor a polynomial, it's often most efficient to look for the roots.
For instance, to factor x^2+5x+6, set it equal to zero and use the quadratic formula. You should determine the roots are x = -2 and x = -3.
Those lead to the factors (x+2) and (x+3). Hence x^2+5x+6 = (x+2)(x+3).
You can use guess-and-check for small values like this, but it gets tricky when trying to factor something like x^2+31x+238.
Anyways, the roots are closely connected to the factorization of the polynomial.
Consider the polynomial equation y = (x^n)+1.
Using the rational root theorem, we see that x = -1 is a potential root.
If x = -1 and n is odd, then x^n+1 = (-1)^(2k+1)+1 = -1*( (-1)^2 )^k+1 = -1+1 = 0 which confirms that x = -1 is a root when n is odd.
x = -1 being a root leads to x+1 being a factor after adding 1 to both sides.
Use a graphing tool like GeoGebra or Desmos to look at the graphs of y = (x^3)+1, y = (x^5)+1, y = (x^7)+1, etc.
All of those graphs have x = -1 as an x intercept and hence (x+1) as a factor.
This will prove (x^n)+1 is composite when n is odd and x is an integer.
By extension it does the same for (a^n)+1.
Here are a few select examples:
n = 3:
a = 2; (a^n)+1 = (2^3)+1 = 9 is composite because 9 = 3*3
a = 3; (a^n)+1 = (3^3)+1 = 28 is composite because 28 = 4*7
a = 4; (a^n)+1 = (4^3)+1 = 65 is composite because 65 = 5*13
n = 5:
a = 2; (a^n)+1 = (2^5)+1 = 33 is composite because 33 = 3*11
a = 3; (a^n)+1 = (3^5)+1 = 244 is composite because 244 = 4*61
a = 4; (a^n)+1 = (4^5)+1 = 1025 is composite because 1025 = 5*205
n = 7:
a = 2; (a^n)+1 = (2^7)+1 = 129 is composite because 129 = 3*43
a = 3; (a^n)+1 = (3^7)+1 = 2188 is composite because 2188 = 4*547
a = 4; (a^n)+1 = (4^7)+1 = 16385 is composite because 16385 = 5*3277
Note that- When a = 2, a+1 = 3 is a factor of (a^n)+1.
- When a = 3, a+1 = 4 is a factor of (a^n)+1.
- When a = 4, a+1 = 5 is a factor of (a^n)+1.
- And so on.
All of what is mentioned is where n is odd. This wraps up the proof.
------------------------------------------------------------
If you're curious what happens when n is even then the graph of y = (x^n)+1 is always above the x axis.
It won't have any real number roots.
The roots will be complex numbers of the form a+bi where i = sqrt(-1)
An example would be y = x^2+49 which has the complex roots 7i and -7i.
So it's not clear if (a^n)+1 is composite or prime when n is even.
Turns out it depends. Here are some examples.
n = 2:
a = 2; (a^n)+1 = (2^2)+1 = 5 is prime (the only factors are 1 and 5)
a = 3; (a^n)+1 = (3^2)+1 = 10 is composite since 2*5 = 10
a = 4; (a^n)+1 = (4^2)+1 = 17 is prime (the only factors are 1 and 17)
n = 4:
a = 2; (a^n)+1 = (2^4)+1 = 17 is prime (the only factors are 1 and 17)
a = 3; (a^n)+1 = (3^4)+1 = 82 is composite since 82 = 2*41
a = 4; (a^n)+1 = (4^4)+1 = 257 is prime (the only factors are 1 and 257; see "primality check" below)
n = 6:
a = 2; (a^n)+1 = (2^6)+1 = 65 = 5*13 is composite
a = 3; (a^n)+1 = (3^6)+1 = 730 = 10*73 is composite
a = 4; (a^n)+1 = (4^6)+1 = 4097 = 17*241 is composite
| Primality Check: To determine if 257 is prime or not, divide it over each item in the list of primes smaller than sqrt(257) = 16.0312You'll divide 257 over the following primes: 2,3,5,7,11, and 13You should find that the result of each division is a non-integer decimal value. This proves none of those values are a factor of 257 and proves 257 is prime. |
Answer by ikleyn(53337)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose a is a natural number >= 2 and n is a natural number larger than 1.
How can I prove that if n is odd, then 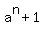 is not a prime? is not a prime?
~~~~~~~~~~~~~~~~~~~~~~~
I edited your post - see the underlined fragment - to make it precisely correct.
If n is an odd positive integer number greater than 1, then there is a decomposition
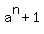 = = 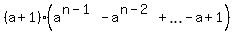 (the signs at degrees of "a" alternate " + " and " - ").
It is a well known formula. To prove it, it is enough to open parentheses.
This formula shows and tells that every integer number of the form
(the signs at degrees of "a" alternate " + " and " - ").
It is a well known formula. To prove it, it is enough to open parentheses.
This formula shows and tells that every integer number of the form 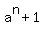 with integer positive " a " and natural odd n > 1 is a composite number.
It is what you want to prove.
with integer positive " a " and natural odd n > 1 is a composite number.
It is what you want to prove.
Solved.
For n=3, the decomposition 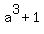 = = 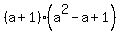 is studied explicitly is studied explicitly
in standard school Math curriculum as the sum of cubes decomposition.
For other odd natural integer " n " greater than 3, it can be
easily obtained from the formula of the sum of a geometric progression
1, -a, a^2, -a^3, a^4, -a^5, . . . , a^(n-1)
with alternate signs, which corresponds to the case of common ratio " -a ".
|
|
|