SOLUTION: Divide (x^5 - a^5) by (x - a) Here is my set up: (x^5 + 0x^4 + 0x^3 + 0x^2 + 0x - a^5)/(x - a) Is this correct?

Algebra ->  Divisibility and Prime Numbers  -> Lessons -> SOLUTION: Divide (x^5 - a^5) by (x - a) Here is my set up: (x^5 + 0x^4 + 0x^3 + 0x^2 + 0x - a^5)/(x - a) Is this correct?       Log On


   

Question 1208348: Divide (x^5 - a^5) by (x - a)

Here is my set up:

(x^5 + 0x^4 + 0x^3 + 0x^2 + 0x - a^5)/(x - a)

Is this correct?

Answer by ikleyn(52756) About Me  (Show Source):
You can put this solution on YOUR website!
.


        It is correct, but it is not a solution and does not lead to the solution. 


The solution is this identity


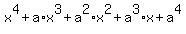    %28x%5E5-a%5E5%29%2F%28x-a%29 = x%5E4+%2B+a%2Ax%5E3+%2B+a%5E2%2Ax%5E2+%2B+a%5E3%2Ax+%2B+a%5E4.


This identity is well known, and it is assumed that a person, to whom this assignment is given, knows it.


This knowledge is the prerequisite for solving this problem.


From your post, I see that you did not know this identity, so you had no the necessary prerequisite.


But after reading my solution, you just know it.


My congratulation.


You may check this identity above by making multiplication.


    (x-a)*(x^4 + a*x^3 + a^2*x^2 + a^^3*x + a^4)) = x^5 - a^5.

This is a whole story.