.
99 consecutive natural numbers, all of which are composite.
What is the smallest number in this set? 100!+2
What is the largest number in this set? 100!+100
What is the method to calculate this? Are my answers correct? Thanks
~~~~~~~~~~~~~~~~~~~~
Your answers are incorrect.
I will construct a sequence of much smaller 99 consecutive natural number, all of which are composite.
First consider all prime numbers lesser than 100:
2, 3, 5, 7, 11, 13, 17, . . . , 89, 97.
Take each of them in maximum degree in a way it is still lesser tnan 100:
2^6 = 64; 3^4 = 81; 5^2 = 25; 7^2 = 49; 11, 13, 17, . . . , 89, 97.
Take the product of these numbers
N =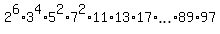 
.
Then 99 consecutive natural numbers
N+2, N+3, N+4, N+5, . . . , N+99, N+100
are
(a) all composite
and
(b) these numbers are less than yours.
Notice, that I do not state that this sequence is minimal; but in any case, it is lesser than yours.
Similar reasoning works for your second question.
