SOLUTION: Use mathematical induction to prove each statement is true for all positive integers n: 5^(n)-1 is divisible by 4 n^(2)-n is divisible by 2

Algebra ->  Divisibility and Prime Numbers  -> Lessons -> SOLUTION: Use mathematical induction to prove each statement is true for all positive integers n: 5^(n)-1 is divisible by 4 n^(2)-n is divisible by 2      Log On


   

Question 1179358: Use mathematical induction to prove each statement is true for all positive integers n:
5^(n)-1 is divisible by 4
n^(2)-n is divisible by 2
Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!


Use mathematical induction to prove each statement is true for all positive integers n:

5^(n)-1 is divisible by 4

n^(2)-n is divisible by 2

==================



n|d means "n divides d"



n=0:  +5%5E%28n%29-1+=+5%5E0-1+=+0,  4 | 0

n=1:   5%5E%28n%29-1+=+5%5E1-1+=+4,  4 | 4



Assume true for n=k: i.e. 4 | %285%5Ek+-+1%29   (hypothesis)



Let n=k+1:  

5%5E%28k%2B1%29-1 

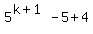
= 5%5E%28k%2B1%29-5%2B4 

= 5%2A5%5Ek-5%2B4

= 5%285%5Ek-1%29%2B4



4 | %285%5Ek-1%29  (by the hypothesis) so 4+ | +5%2A%285%5Ek-1%29 as well.



Therefore, +4+ | 5%285%5Ek-1%29%2B4 (if 4|P then 4|(P+4)) 

and the proof is complete.





======



The other proof does not require induction n%5E2-n+ is always even, which is divisible by 2.   Follow the steps I did in first problem if you must have a proof by induction (show true for base case, assume hypothesis (n=k), and then show it leads to truth of the step case where n=k+1)