Question 1177319: Let n=355,813,6de be a base-ten numeral with d and e its last two digits. Give all of the choices of the two-digit numbers de for which n is divisible by 12.
Found 2 solutions by Edwin McCravy, MathLover1:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We form the smallest potential value for de which is 10, the smallest
two-digit number.
If de were equal to 10 we would have an integer when we divided
n=355813610 by 12. But we get 29651134.17, which is not an integer.
So we go to the next integer above 29651134.17, which is 29651135, and
multiply it by 12 and we get 355813620, which is divisible by 12.
So we have 355813620, so that's a choice of de = 20
We add 12 to that to get the next multiple of 12:
355813620 + 12 = 355813632, so that's a choice of de = 32
We add 12 to that to get the next multiple of 12
355813632 + 12 = 355813644, so that's a choice of de = 44
We add 12 to that to get the next multiple of 12
355813644 + 12 = 355813656, so that's a choice of de = 56
We add 12 to that to get the next multiple of 12
355813656 + 12 = 355813668, so that's a choice of de = 68
We add 12 to that to get the next multiple of 12
355813668 + 12 = 355813680, so that's a choice of de = 80
We add 12 to that to get the next multiple of 12
355813680 + 12 = 355813692, so that's a choice of de = 92
That's as far as we can go, for adding 12 to that would change
the 3rd digit from the right to a 7. But it must remain 6.
So all the choices for de are 20, 32, 44, 56, 68, 80, and 92.
Edwin
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!  is divisible by is divisible by 
 must be divisible by must be divisible by  and and 
A number is divisible by  if the sum of the digits is divisible by if the sum of the digits is divisible by 
A number is divisible by  if the last if the last digits are divisible by digits are divisible by 

the sum of the digits is 
so de must be divisible by  and and

choices for  : :
 ......................... ......................... , ,  => => 
 ......................... ......................... , ,  => => 
 ......................... ......................... , ,  => => 
 ......................... ......................... , ,  => => 
 ......................... ......................... , ,  => => 
 ......................... ......................... , ,  => => 
 ......................... ......................... , , => => 
 ......................... ......................... , , => => 
so, all the choices for de are  , , , ,  , ,  , ,  , , 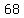 , ,  , and , and 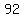
|
|
|