Tutors Answer Your Questions about Divisibility and Prime Numbers (FREE)
Question 1209383: Prove that n^2-n is always even
Found 2 solutions by greenestamps, math_tutor2020:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The statement of the problem is deficient; n^2-n is NOT always even. It is always even IF n IS AN INTEGER.
n^2-n = n(n-1)
If n is an integer, then that expression is the product of two consecutive integers. In any two consecutive integers, one of them is odd and the other is even; and the product of two integers is even whenever at least one of them is even.
So the product of two consecutive integers is always even.
TRUE: n^2-n is always even if n is an integer
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I assume that n is an integer.
With many integer proofs, we break things up into two cases.
We see what happens when n is even and when n is odd.
If n is even then we'd have n = 2k, where k is some integer.
Then we could say,
n^2-n
= (2k)^2-2k
= 4k^2-2k
= 2*(2k^2-k)
= 2*(some integer)
= even integer
We have shown that n^2-n is even when n is even.
If n is odd then it means n = 2k+1
Which leads to...
n^2-n
= (2k+1)^2-(2k+1)
= (4k^2+4k+1)-(2k+1)
= 4k^2+4k+1-2k-1
= 4k^2+2k
= 2*(2k^2+k)
= 2*(some integer)
= even integer
This proves that n^2-n is even despite n being odd.
Regardless if n is even or odd, n^2-n is always even.
Therefore n^2-n is always even for any integer n.
The proof is complete.
----------
Here is a faster alternative proof method.
n^2-n = n(n-1)
Either n is even or n-1 is even
By "or", I refer to "exclusive or".
So either n = 2k or n-1 = 2k
2 is buried somewhere in the factorization of n(n-1)
This proves n^2-n is even regardless of any integer you pick for n.
----------
Let's generate a few examples trying n = 1 through n = 5.
n^2-n = 1^2-1 = 1-1 = 0
n^2-n = 2^2-2 = 4-2 = 2
n^2-n = 3^2-3 = 9-3 = 6
n^2-n = 4^2-4 = 16-4 = 12
n^2-n = 5^2-5 = 25-5 = 20
I encourage you to try other examples.
Recall that a number is even (i.e. a multiple of 2) when the number ends with 0, 2, 4, 6 or 8.
The examples on their own do not constitute a formal proof since we'd need to check infinitely many examples. However, they are useful to help solidify understanding.
Question 1209362: There are 830 composite numbers less than 1000. Let S be the set of composite numbers smaller than 1000 that are not divisible by 2, 3, or 7. How many elements does S have?
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 120
-----------------------------------------------
Explanation
To find the solution, we'll need the floor function.
This function rounds a positive decimal number down to the nearest integer.
Think of it like a vertical number line.
As the name "floor" implies, we move down to the floor to magnetically lock onto the nearest integer.
Examples:
floor(2.1) = 2
floor(7.9999999) = 7
It might be tempting to round 7.9999999 to 8, but just remember we round down to the floor.
It doesn't matter how close to the ceiling the input is.
Basically the floor function chops off the decimal when looking at positive numbers only.
If the input is an integer, then no changes are made.
There are 999 values in the set {1,2,3,...,999}- Floor(999/2) = 499 of those values are multiples of 2.
- Floor(999/3) = 333 of those values are multiples of 3.
- Floor(999/7) = 142 of those values are multiples of 7.
- Floor(999/(2*3)) = 166 of those values are multiples of 2*3 aka 6.
- Floor(999/(2*7)) = 71 of those values are multiples of 2*7 aka 14.
- Floor(999/(3*7)) = 47 of those values are multiples of 3*7 aka 21.
- Floor(999/(2*3*7)) = 23 of those values are multiples of 2*3*7 aka 42.
Use the inclusion-exclusion principle to say,
499+333+142-166-71-47+23 = 713
A Venn Diagram may come in handy.
If we define P as the set of positive integers smaller than 1000 that are multiples of 2, 3, or 7, then there are 713 values in set P.
Here are the first few items of set P
2,3,4,6,7,8,9,10,12,14,15,16,18,20,21,22
There are 3 prime numbers in set P. Those values are 2,3,7
The remaining 713-3 = 710 items are composite since they are multiples of those trio of values mentioned.
The instructions tell us there are 830 composite numbers in the set {1,2,3,4,...,999}.
Note that 1 isn't composite and it's not prime either.
So there are 830-710 = 120 values in set S.
I have verified the answer is correct using a Python script.
You can take this route as well, or you can use a spreadsheet to verify the answer.
If you aren't given the 830 figure, then you can consult a list of primes to determine there are 168 primes in the set {2,3,...,999}. So that means there are 998-168 = 830 composite numbers in the set {2,3,...,999}. I've excluded the value "1" since it's neither prime nor composite.
The first few values in set S would be 25,55,65,85,95,115,121,125
Question 1209285: Find the LCM of 7, 10, 12, 15, 24, 75
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 4200
----------------------------------------------------------
Explanation
I'll discuss 4 methods
Method 1
Find the prime factorization of each value.
If the original value is prime, then just say "1 times that number" even though 1 itself isn't prime.
7 = 1*7
10 = 2*5
12 = 2*2*3
15 = 3*5
24 = 2*2*2*3
75 = 3*5*5
The unique prime factors mentioned were: 2,3,5,7
For any given row,- 2 shows up at most three times to contribute 2^3 as part of the LCM.
- 3 shows up at most once to contribute 3^1
- 5 shows up at most twice to contribute 5^2
- 7 shows up at most once to contribute 7^1
The LCM is therefore (2^3)*(3^1)*(5^2)*(7^1) = 4200
Many online LCM calculators can be used to verify the answer.
If you are using Desmos then the command to type in is lcm(7, 10, 12, 15, 24, 75)
The "lcm" must be all lowercase. Do not use curly braces.
------------------------
Method 2
Let's say we only worried about finding the LCM of the set of two values {x,y}
We have a very useful formula that connects the LCM and GCF of two numbers.
LCM = x*y/GCF
where "LCM" refers to "LCM of x and y"; and "GCF" refers to "GCF of x and y".
That formula is going to be used repeatedly since we have more than two numbers in the original set.
Let's find the LCM of the subset {7,10} which are the first two items of the original set.
LCM = x*y/GCF
LCM = 7*10/1
LCM = 70
The LCM of {7,10} is 70
Replace "7,10" in the original set with "70"
{7, 10, 12, 15, 24, 75} shrinks to {70, 12, 15, 24, 75}
Then we do another LCM calculation on the first two items of this shrunken set.
LCM = x*y/GCF = 70*12/2 = 420
The LCM of the subset {70,12} is 420.
Replace "70,12" with "420"
{70, 12, 15, 24, 75} shrinks to {420, 15, 24, 75}
It's a somewhat slow process but we are steadily shrinking the set down.
Keep the process going until there's one number remaining.
You should arrive at 4200
------------------------
Method 3
I'll use the Cake method discussed on this page
Read that page first to see how the method works. Other names for it could be "ladder method", "factor box method", or "grid method". Perhaps there might be other names.
Here's the scratch work when using the Cake Method.
| (1) | 7 | 10 | 12 | 15 | 24 | 75 | | (2) | 7 | 5 | 6 | 15 | 12 | 75 | | (2) | 7 | 5 | 3 | 15 | 6 | 75 | | (3) | 7 | 5 | 1 | 5 | 2 | 25 | | (5) | 7 | 1 | 1 | 1 | 2 | 5 | | (7) | (1) | (1) | (1) | (2) | (5) |
p = multiply the left column of parenthesis values: 1*2*2*3*5 = 60
q = multiply the bottom row of parenthesis values: 7*1*1*1*2*5 = 70
LCM = p*q = 60*70 = 4200
Ignoring the (1), the first row is the original set of values. The (1) off to the left is optional but I find it helps with consistency.
The second row is where I divide even values by 2 (eg: 10/2 = 5). The (2) off to the left keeps track of what I divided the row by. If a value is not a multiple of 2, then leave it as is.
The third row is the same idea. We divide by another 2 since 6 and 12 have this as a common factor.
Once reaching "7, 5, 1, 5, 2, 25" it's clear that 2 is not a common factor of any pairing. So we then divide by 3, and then by 5, and so on. We only need to check up to the prime 7.
The bottom row of values in parenthesis is optional, but I find it helps with consistency.
----------------
Method 4
The Division Table method is very similar to the Cake method.
Here's the scratch work
| (1) | 7 | 10 | 12 | 15 | 24 | 75 | | (2) | 7 | 5 | 6 | 15 | 12 | 75 | | (2) | 7 | 5 | 3 | 15 | 6 | 75 | | (2) | 7 | 5 | 3 | 15 | 3 | 75 | | (3) | 7 | 5 | 1 | 5 | 1 | 25 | | (5) | 7 | 1 | 1 | 1 | 1 | 5 | | (5) | 7 | 1 | 1 | 1 | 1 | 1 | | (7) | 1 | 1 | 1 | 1 | 1 | 1 |
Collect all the items in parenthesis to multiply together:
LCM = 1*2*2*2*3*5*5*7 = 4200
The Division Table method is discussed on this page. Each item in a parenthesis tells us what I divided some of the row items by. The goal of this method is to get nothing but 1's in the bottom row.
---------------
Technically there's a 5th alternate route of listing the multiples of each item to see what they have in common.
However, this is NOT recommended since the LCM (4200) is very large.
You'll be listing a lot of multiples. Perhaps a spreadsheet is best suited for a task like this. Even then it would be tedious busy-work in my opinion.
Question 1207615: As shown in class, the Euclidean algorithm can be used to find solutions to equations of the form
\[ax + by = c.\]
Use the Euclidean algorithm to find integers $x$ and $y$ such that $5x + 2y = 1,$ with the smallest possible positive value of $x$.
State your answer as a list with $x$ first and $y$ second, separated by a comma.
Note that while there are many pairs of integers $x$ and $y$ that satisfy this equation, there is only one pair that comes from using the Euclidean algorithm as described in class, and this pair solves the problem.
Answer by CPhill(1959)   (Show Source): (Show Source):
Question 1208953: Suppose a >= 2 and n is a natural number larger than 1.
How can I prove that if n is odd, then a^n+1 is not prime?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose a is a natural number >= 2 and n is a natural number larger than 1.
How can I prove that if n is odd, then 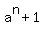 is not a prime? is not a prime?
~~~~~~~~~~~~~~~~~~~~~~~
I edited your post - see the underlined fragment - to make it precisely correct.
If n is an odd positive integer number greater than 1, then there is a decomposition
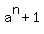 = = 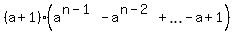 (the signs at degrees of "a" alternate " + " and " - ").
It is a well known formula. To prove it, it is enough to open parentheses.
This formula shows and tells that every integer number of the form
(the signs at degrees of "a" alternate " + " and " - ").
It is a well known formula. To prove it, it is enough to open parentheses.
This formula shows and tells that every integer number of the form 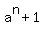 with integer positive " a " and natural odd n > 1 is a composite number.
It is what you want to prove.
with integer positive " a " and natural odd n > 1 is a composite number.
It is what you want to prove.
Solved.
For n=3, the decomposition 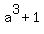 = = 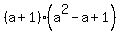 is studied explicitly is studied explicitly
in standard school Math curriculum as the sum of cubes decomposition.
For other odd natural integer " n " greater than 3, it can be
easily obtained from the formula of the sum of a geometric progression
1, -a, a^2, -a^3, a^4, -a^5, . . . , a^(n-1)
with alternate signs, which corresponds to the case of common ratio " -a ".
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
It wasn't stated, but I'm assuming 'a' is an integer.
I'll also assume the +1 is not in the exponent.
If the +1 was in the exponent, then it's very easy to show that a^(n+1) is always composite regardless if n was even or odd.
To factor a polynomial, it's often most efficient to look for the roots.
For instance, to factor x^2+5x+6, set it equal to zero and use the quadratic formula. You should determine the roots are x = -2 and x = -3.
Those lead to the factors (x+2) and (x+3). Hence x^2+5x+6 = (x+2)(x+3).
You can use guess-and-check for small values like this, but it gets tricky when trying to factor something like x^2+31x+238.
Anyways, the roots are closely connected to the factorization of the polynomial.
Consider the polynomial equation y = (x^n)+1.
Using the rational root theorem, we see that x = -1 is a potential root.
If x = -1 and n is odd, then x^n+1 = (-1)^(2k+1)+1 = -1*( (-1)^2 )^k+1 = -1+1 = 0 which confirms that x = -1 is a root when n is odd.
x = -1 being a root leads to x+1 being a factor after adding 1 to both sides.
Use a graphing tool like GeoGebra or Desmos to look at the graphs of y = (x^3)+1, y = (x^5)+1, y = (x^7)+1, etc.
All of those graphs have x = -1 as an x intercept and hence (x+1) as a factor.
This will prove (x^n)+1 is composite when n is odd and x is an integer.
By extension it does the same for (a^n)+1.
Here are a few select examples:
n = 3:
a = 2; (a^n)+1 = (2^3)+1 = 9 is composite because 9 = 3*3
a = 3; (a^n)+1 = (3^3)+1 = 28 is composite because 28 = 4*7
a = 4; (a^n)+1 = (4^3)+1 = 65 is composite because 65 = 5*13
n = 5:
a = 2; (a^n)+1 = (2^5)+1 = 33 is composite because 33 = 3*11
a = 3; (a^n)+1 = (3^5)+1 = 244 is composite because 244 = 4*61
a = 4; (a^n)+1 = (4^5)+1 = 1025 is composite because 1025 = 5*205
n = 7:
a = 2; (a^n)+1 = (2^7)+1 = 129 is composite because 129 = 3*43
a = 3; (a^n)+1 = (3^7)+1 = 2188 is composite because 2188 = 4*547
a = 4; (a^n)+1 = (4^7)+1 = 16385 is composite because 16385 = 5*3277
Note that- When a = 2, a+1 = 3 is a factor of (a^n)+1.
- When a = 3, a+1 = 4 is a factor of (a^n)+1.
- When a = 4, a+1 = 5 is a factor of (a^n)+1.
- And so on.
All of what is mentioned is where n is odd. This wraps up the proof.
------------------------------------------------------------
If you're curious what happens when n is even then the graph of y = (x^n)+1 is always above the x axis.
It won't have any real number roots.
The roots will be complex numbers of the form a+bi where i = sqrt(-1)
An example would be y = x^2+49 which has the complex roots 7i and -7i.
So it's not clear if (a^n)+1 is composite or prime when n is even.
Turns out it depends. Here are some examples.
n = 2:
a = 2; (a^n)+1 = (2^2)+1 = 5 is prime (the only factors are 1 and 5)
a = 3; (a^n)+1 = (3^2)+1 = 10 is composite since 2*5 = 10
a = 4; (a^n)+1 = (4^2)+1 = 17 is prime (the only factors are 1 and 17)
n = 4:
a = 2; (a^n)+1 = (2^4)+1 = 17 is prime (the only factors are 1 and 17)
a = 3; (a^n)+1 = (3^4)+1 = 82 is composite since 82 = 2*41
a = 4; (a^n)+1 = (4^4)+1 = 257 is prime (the only factors are 1 and 257; see "primality check" below)
n = 6:
a = 2; (a^n)+1 = (2^6)+1 = 65 = 5*13 is composite
a = 3; (a^n)+1 = (3^6)+1 = 730 = 10*73 is composite
a = 4; (a^n)+1 = (4^6)+1 = 4097 = 17*241 is composite
| Primality Check: To determine if 257 is prime or not, divide it over each item in the list of primes smaller than sqrt(257) = 16.0312You'll divide 257 over the following primes: 2,3,5,7,11, and 13You should find that the result of each division is a non-integer decimal value. This proves none of those values are a factor of 257 and proves 257 is prime. |
Question 1208954: not sure how to prove this?
if n is odd then n^2 = 1 (mod 4)
thanks!
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
not sure how to prove this?
if n is odd then n^2 = 1 (mod 4)
thanks!
~~~~~~~~~~~~~~~~~~~~
It is easy.
If n is odd integer number, it can be presented in the form n = 2k+1,
where k is some integer number.
Then
n^2 = (2k)^2 + 2*(2k) + 1 = 4k^2 + 4k + 1. (1)
In the right side, first addend, 4k^2, is a multiple of 4,
and the second addend 4k is a multiple of k.
Hence, the sum of the first two addends is a multiple of k.
Thus n^2 = 1 (mod 4).
At this point, the proof is complete.
In whole, this all is at the level of self-evident truths.
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
n = an odd integer
n = 2k+1 for some integer k
n^2 = (2k+1)^2
n^2 = 4k^2+4k+1 after using the FOIL rule
n^2 = 4*(k^2+k) + 1
n^2 = 4*integer + 1
The last equation shows that whatever n^2 happens to be, it's 1 more than a multiple of 4. This only applies when n is odd.
We have shown that (n^2)/4 gives some quotient remainder 1 when n is odd.
And also proves n^2 = 1 (mod 4) when n is odd.
Some examples.
| n | n^2 | (n^2)/4 | n^2 (mod 4) | | 1 | 1 | 0 remainder 1 | 1 | | 3 | 9 | 2 remainder 1 | 1 | | 5 | 25 | 6 remainder 1 | 1 | | 7 | 49 | 12 remainder 1 | 1 | | 9 | 81 | 20 remainder 1 | 1 | | 11 | 121 | 30 remainder 1 | 1 |
Try some other examples out for yourself.
When doing modular arithmetic, we ignore the quotient to focus on the remainder only.
Extra Credit Question: Try to prove that n^2 = 0 (mod 4) when n is even. A hint is that n = 2k.
Question 1208752: Show that x^2 + 7x + 13 is prime.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Show that x^2 + 7x + 13 is prime.
~~~~~~~~~~~~~~~~~~
The precise meaning of this question is dark and unclear.
Therefore, I will re-formulate the request, to make it sensible.
Show that polynomial x^2 + 7x + 13 is a prime polynomial
in the ring of polynomials with real coefficients.
The solution is simple and beautiful, both at the same time.
Had the polynomial be non-prime (= composite) in this ring,
it would be a product of two polynomials of degree 1, i.e. linear binomials
x^2 + 7x + 13 = (ax+b)*(cx+d).
In this case, the polynomial would have real roots  and and  .
But the polynomial x^2 + 7x + 13 has a negative discriminant
d = .
But the polynomial x^2 + 7x + 13 has a negative discriminant
d =  = = 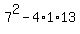 = 49 - 52 = -5.
It means that this polynomial has no real roots.
This contradiction proves that the given polynomial is a prime polynomial
in the ring of polynomials with real coefficients. = 49 - 52 = -5.
It means that this polynomial has no real roots.
This contradiction proves that the given polynomial is a prime polynomial
in the ring of polynomials with real coefficients.
Solved.
The same reasoning works for polynomials with rational coefficients or/and for
polynomials with integer coefficients.
---------------------
I don't know what is your level in Math - therefore, I fully admit that you
may understand nothing from my explanation.
Why I may think so - because the problem in your post is worded mathematically incorrectly.
On the other hand, since you brought this problem, I may assume that you have all
the necessary pre-requisites to understand my solution.
The rest depends on you - not on me.
With the full context, this problem is for the first year undergraduate university
Math student, who recently started learning Abstract Algebra.
Such a student should understand my solution adequately.
Question 1208751: Show that x^2 + 3 is prime.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Show that x^2 + 3 is prime.
~~~~~~~~~~~~~~~~~~
The precise meaning of this question is dark and unclear.
Therefore, I will re-formulate the request, to make it sensible.
Show that polynomial x^2 + 3 is a prime polynomial
in the ring of polynomials with real coefficients.
The solution is simple and beautiful, both at the same time.
Had the polynomial be non-prime (= composite) in this ring,
it would be a product of two polynomials of degree 1, i.e. linear binomials
x^2 + 3 = (ax+b)*(cx+d).
In this case, the polynomial would have real roots  and and  .
But the polynomial x^2 + 3 has always positive values for all real values of x,
since x^2 is always non-negative, while the addend "3" is a positive constant.
This contradiction proves that the given polynomial is a prime polynomial
in the ring of polynomials with real coefficients. .
But the polynomial x^2 + 3 has always positive values for all real values of x,
since x^2 is always non-negative, while the addend "3" is a positive constant.
This contradiction proves that the given polynomial is a prime polynomial
in the ring of polynomials with real coefficients.
Solved.
The same reasoning works for polynomials with rational coefficients or/and for
polynomials with integer coefficients.
---------------------
I don't know what is your level in Math - therefore, I fully admit that you
may understand nothing from my explanation.
Why I may think so - because the problem in your post is worded mathematically incorrectly.
On the other hand, since you brought this problem, I may assume that you have all
the necessary pre-requisites to understand my solution.
The rest depends on you - not on me.
With the full context this problem is for the first year undergraduate university
Math student, who recently started learning Abstract Algebra.
Such a student should understand my solution adequately.
Question 1208631: What is the greatest prime you must consider to test whether 4755 is prime?
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To check whether 4755 is a prime, you should test all primes lesser than 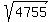 = 68.95... = 68.95...
The greatest prime from this list is 67.
Why it is so, read and learn from these Internet links
https://en.wikipedia.org/wiki/Primality_test
https://en.wikipedia.org/wiki/Primality_test
or read any fundamental course on Number theory.
Question 1208348: Divide (x^5 - a^5) by (x - a)
Here is my set up:
(x^5 + 0x^4 + 0x^3 + 0x^2 + 0x - a^5)/(x - a)
Is this correct?
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is correct, but it is not a solution and does not lead to the solution.
The solution is this identity
 = = 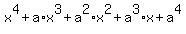 .
This identity is well known, and it is assumed that a person, to whom this assignment is given, knows it.
This knowledge is the prerequisite for solving this problem.
From your post, I see that you did not know this identity, so you had no the necessary prerequisite.
But after reading my solution, you just know it.
My congratulation.
You may check this identity above by making multiplication.
(x-a)*(x^4 + a*x^3 + a^2*x^2 + a^^3*x + a^4)) = x^5 - a^5. .
This identity is well known, and it is assumed that a person, to whom this assignment is given, knows it.
This knowledge is the prerequisite for solving this problem.
From your post, I see that you did not know this identity, so you had no the necessary prerequisite.
But after reading my solution, you just know it.
My congratulation.
You may check this identity above by making multiplication.
(x-a)*(x^4 + a*x^3 + a^2*x^2 + a^^3*x + a^4)) = x^5 - a^5.
This is a whole story.
Question 1207857: Find all integers  , ,  , such that , such that  is its own inverse modulo is its own inverse modulo 
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find all integers  , {0 <= n < 163}, such that n is its own inverse modulo 163. , {0 <= n < 163}, such that n is its own inverse modulo 163.
~~~~~~~~~~~~~~~~~~~~
(a) For our solution, the important fact is that 163 is a prime number.
Integer x is an inverse to integer n modulo 163 if and only if
nx = 1 mod 163 by the definition.
According to it, integer n is its own inverse modulo 163 if and only if
n^2 = 1 modulo 163.
One solution is trivial: it is n = 1 mod 163, or simply n= 1.
It is easy to find another (non-trivial) solution n. Take n = -1 mod 163; then n^2 = (-1)*(-1) = 1 mod 163.
So, the class n = -1 mod 163 is the other possible solution.
If we want n in the interval 0 <= n < 163, we should take n = 162, which is 163-1.
Then we have n^2 = (163-1)*(163-1) = 163^2 - 2*163 + 1 = 1 mod 163.
So, this part (one half) of the problem is solved.
We found two solutions in the given interval: n = 1 and n = 162.
(b) Now we want to prove that these two solutions, n= 1 and n= 162, are unique in the given interval
OK. Let assume that m is another integer number in the interval 0 <= m < 163,
inverse to itself mod 163. Then we have these two modular equations
m*m = 1 mod 163
1*1 = 1 mod 163.
Taking the difference, we have
(m+1)*(m-1) = 0 mod 163.
It means that either (m-1) or (m+1) is divisible by 163.
In combination with the fact that 0 <= m < 163, it means that either m= 1 or m= 162.
Thus we proved that in interval [0,163) there is no other own-inverse numbers mod 163
Solved, with complete explanations.
---------------------
This problem is from 22nd Philippine Mathematical Olympiad of 2019.
Question 1207737: Carlos wants to send Cecil a message encrypted with RSA. Cecil has published his public encryption exponent $4$ and his public modulus $15$. When Carlos encrypts the number $11$ with this system, what is the result?
Found 2 solutions by math_tutor2020, Edwin McCravy:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor Edwin has a great solution.
I'll show another way to compute 11^4 (mod 15).
First let's determine 11^2 in mod 15.
11^2 = 121 = 1 (mod 15)
How did I go from 121 to 1?
Well notice that 121/15 = 8 remainder 1
Ignore the quotient. All we care about is the remainder with modular arithmetic.
Both 121 and 1 have the same remainder when dividing over 15.
So that's how 121 = 1 (mod 15)
Side note: If a = b (mod n), then a-b is a multiple of n. In other words, a-b = nk for some integer k.
In the claim above we have 121-1 = 120 as a multiple of 15 (since 15*8 = 120).
Then,
11^2 = 1 (mod 15)
(11^2)^2 = 1^2 (mod 15)
11^(2*2) = 1 (mod 15)
11^4 = 1 (mod 15)
Dividing 11^4 over 15 gives some quotient with remainder 1.
You can use long division to check this claim as Edwin has done.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Question 1207738: The House of Lilliput is using RSA encryption to receive secret messages from all the realms. They have published their public encoding exponent $e = 2$ and their public modulus $M = pq = 15$.
Break the code: Find their secret decoding exponent $d.$
Found 2 solutions by ikleyn, Alan3354:
Answer by ikleyn(52780)   (Show Source): (Show Source):
Answer by Alan3354(69443)   (Show Source): (Show Source):
Question 1207739: Find an integer $x$ such that $0 \leq x < 205$ and $x^2 \equiv 11 \pmod{205}$.
Found 2 solutions by math_tutor2020, greenestamps:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
See this similar question before moving on
https://www.algebra.com/algebra/homework/divisibility/Divisibility_and_Prime_Numbers.faq.question.1207682.html
I'll use the ideas discussed in that link.
phi(n) = Euler's Totient function
phi(205) = phi(5*41)
phi(205) = phi(5)*phi(41)
phi(205) = (5-1)*(41-1)
phi(205) = 160
There are 160 integers in the set {1,2,3,...,203,204} such that they are relatively prime to 205.
The goal of solving
x^2 = 11 (mod 205)
will have us needing to solve
2u = 1 (mod 160)
which turns into
2u-1 = 160k
and then can be arranged into
2(u-80k) = 1
The left hand side is always even, but the right hand side is odd.
This mismatch proves 2u-1 = 160k has no integer solutions
This means 2u = 1 (mod 160) doesn't have any solutions either.
Ultimately x^2 = 11 (mod 205) doesn't have any solutions.
You can use spreadsheet software or a coding script like python to verify.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A quick check with an excel spreadsheet shows that there is no answer, so there is no sense looking for a mathematical way to find the answer.
Question 1207736: An eccentric baseball card collector wants to distribute her collection among her descendants. If she divided her cards among her 10 great-great-grandchildren, there would be 6 cards left over. If she divided her cards among her 7 great-grandchildren, there would be 5 cards left over. If she divided her cards among her 3 grandchildren, there would be 2 cards left over. If she divided her cards among her 2 children, there would be 0 cards left over.
What is the smallest possible number of cards in her collection?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) If she divided her cards among her 10 great-great-grandchildren, there would be 6 cards left over.
The number of cards can be 6, 16, 26, 36, 46, ...
(2) If she divided her cards among her 7 great-grandchildren, there would be 5 cards left over.
The number of cards can be 26, 96, 166, 236, ...
(3) If she divided her cards among her 3 grandchildren, there would be 2 cards left over.
The number of cards can be 26, 236, 446, ...
(4) If she divided her cards among her 3 grandchildren, there would be 2 cards left over.
This is already taken care of by (1).
ANSWER: 26
Question 1207735: Greg finds the value of 708*709*710*711 and then divides the result over 712. What is the remainder? Is it possible to do this using mental math only?
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
This is possible without a calculator.
It can be done really quickly after you get enough practice.
708 is 4 short of 712, so we can say 708 = -4 (mod 712).
The "mod" refers to "modular arithmetic".
It is very useful when dealing with remainders.
709 is 3 short of 712, so 709 = -3 (mod 712).
And so on.
Therefore 708*709*710*711= (-4)*(-3)*(-2)*(-1) = 24 (mod 712)
Whatever massive number 708*709*710*711 turns out to be, dividing it over 712 yields some quotient with remainder 24.
Throughout the modular arithmetic process, we ignore the quotient.
Answer: 24
Question 1207719: Let $m$ and $n$ be non-negative integers. If $m = 6n + 2$, then what integer between $0$ and $m$ is the inverse of $2$ modulo $m$? Answer in terms of $n$.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll follow a similar line of thinking as the other tutor, but show a slightly different pathway.
Let x be some integer in the set {0,1,2,3,...,m-2,m-1} such that 2x = 1 (mod m), assuming such a value exists.
x is the multiplicative inverse of 2 in mod m
This converts to 2x-1 = km for some integer k.
The general rule is that if a = b (mod n) then a-b is a multiple of n, i.e. a-b = kn for some integer k.
Rephrased: a & b generate the same remainder when dividing by n.
That slight tangent aside, let's revisit 2x-1 = km to apply a substitution.
2x-1 = k*m
2x-1 = k(6n+2) ......... plug in m = 6n + 2
2x-1 = 2k(3n+1)
2x - 2k(3n+1) = 1
2(x - k(3n+1) ) = 1
2(some integer) = 1
The left hand side on the last line is always even, but the right hand side is odd. This contradiction proves that there aren't any integer solutions to 2x-1 = km where m = 6n+2.
By extension, there aren't any solutions to 2x = 1 (mod m) either.
2 does not have a multiplicative inverse in mod m.
Answer: No solutions.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let m and n be non-negative integers. If m = 6n + 2, then what integer between 0 and m
is the inverse of 2 modulo m? Answer in terms of n.
~~~~~~~~~~~~~~~~~~~~~~
Notice that m = 6n+2 is an even integer number, for any integer number n.
Let's assume that an integer x between 0 and m is the inverse of 2 modulo m.
It means that 2*x = 1 mod m, which is the same as to say that
2x - 1 is a multiple of m : 2x - 1 = k*m.
But 2x is an even number, and k*m is an even number, since "m" is even.
Therefore, this equality 2x - 1 = km is not possible with integer x and "k".
Hence, there is NO any integer between 0 and m which is inverse of 2 modulo m.
ANSWER. There is NO any integer between 0 and m which is inverse of 2 modulo m.
Solved.
---------------
What I proved in my post, in terms of abstract algebra is THIS general statement:
In the ring of integers modulo m, Z/m, where " m " is an even number,
the class {2 mod m} is NOT an invertible element.
In opposite, in such a ring, the class {2 mod m} is a divisor of zero;
and it is well known fact of abstract algebra that in a ring a divisor of zero can not be invertible.
Question 1207720: Find the number of solutions to
N &\equiv 2 \pmod{5}, \\
N &\equiv 2 \pmod{6}, \\
N &\equiv 2 \pmod{7}
in the interval 0 \le N < 1000.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The numbers are 2 more than a multiple of either 5, 6, or 7.
Since 5, 6, and 7 have no common factors, the numbers have to be 2 more than a multiple of 5*6*7=210.
The numbers N satisfying that requirement in the interval [0,1000] are 2, 212, 422, 632, and 842.
ANSWER: 5 solutions
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the number of solutions to
N = {2 mod 5},
N = {2 mod 6},
N = {2 mod 7}.
~~~~~~~~~~~~~~~~~~~~~~~
Consider the number N-2.
N-2 = {0 mod 5},
N-2 = {0 mod 6}
and
N-2 = {0 mod 7}.
It means that N-2 is a multiple of 5, 6 and 7, at the same time.
The integer numbers N-2 in the interval [-2,998] divisible by 5, 6 and 7
at the same time are those multiple of 210, i.e. 0, 210, 420, 630, 840.
Hence, the solutions N under the problem's question are the numbers 2, 212, 422, 632, 842.
In all, there are 5 solutions. ANSWER
Solved.
Question 1207721: Find the smallest positive integer $N$ such that
N &\equiv 2 \pmod{5}, \\
N &\equiv 2 \pmod{7}.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
N is the smallest positive integer that is both 2 more than a multiple of 5 and 2 more than a multiple of 7.
The answer, trivially, is N=2.
ANSWER: 2
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the smallest positive integer N such that
N = {2 mod 5},
N = {2 mod 7}.
~~~~~~~~~~~~~~~~~~~~~~~
See the solution by @greenestamps.
Question 1207684: Find all integers $n$, $0 \le n < 163$, such that $n$ is its own inverse modulo $8.$
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor ikleyn has pointed out that n^2 = 1 (mod 8) has solutions:
n = 1, n = 3, n = 5, n = 7
The interesting thing is that the n = 1 and n = 7 cases pair up.
Notice how n = 7 is one short of 8, so we can think of it like n = -1 in mod 8.
Squaring -1 will generate +1 or simply 1.
Similarly, the n = 3 and n = 5 cases pair up together.
Notice n = 5 is three short of 8, in which we can think of it like n = -3 (mod 8). Squaring this leads to +9 = 9 = 1 (mod 8).
--------------------------------------------------------------------------
Slight tangent aside, the four classes of solutions were
n = 1, n = 3, n = 5, n = 7
Your teacher is asking you to look through the interval  to see which of those values of n work or not. to see which of those values of n work or not.
Let's focus on the n = 1 case.
This is when the numbers are of the form 8k+1, since each produces remainder 1 in mod 8.
Look at a few values of k.
n = 8k+1 = 8*0+1 = 1
n = 8k+1 = 8*1+1 = 9
n = 8k+1 = 8*2+1 = 17
n = 8k+1 = 8*3+1 = 25
Another way to generate this sequence is to start at 1, and add 8 to each term.
The question is now: when does this subsequence stop?
Let's set it equal to 163 and see what happens.
8k+1 = 163
8k = 163-1
8k = 162
k = 162/8
k = 20.25
If k = 20 then 8k+1 = 8*20+1 = 161
If k = 21 then 8k+1 = 8*21+1 = 167
Therefore the highest we can go in this congruence class is 161.
All of these values
{1, 9, 17, ..., 153, 161}
fit the n = 1 congruence class and are a subset of the overall solution space.
When dividing each of those items over 8, we'll get some quotient with remainder 1.
You will follow similar ideas for n = 3, n = 5, and n = 7.
I'll let the student determine those.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find all integers n, 0 < n < 163, such that n is its own inverse modulo 8.
~~~~~~~~~~~~~~~~~
n is own inverse modulo 8 means
n*n = 1 mod 8.
We consider numbers n modulo 8, so, it is enough to consider
the congruence classes from {1 mod 8} to {7 mod 8}.
n= 1: n*n = 1*1 = 1 mod 8. Hence, n= 1 works.
n= 2: n*n = 2*2 = 4 mod 8. Hence, n= 2 does not work.
n= 3: n*n = 3*3 = 1 mod 8. Hence, n= 3 works.
n= 4: n*n = 4*4 = 16 = 0 mod 8. Hence, n= 4 does not work.
n= 5: n*n = 5*5 = 1 mod 8. Hence, n= 5 works.
n= 6: n*n = 6*6 = 36 = 4 mod 8. Hence, n= 6 does not work.
n= 7: n*n = 7*7 = 49 = 1 mod 8. Hence, n= 7 works.
ANSWER. Among the congruence classes mod 8, classes 1, 3, 5 and 7 work as own inverses mod 8.
the rest of classes do not work as own inverses mod 8.
Solved.
/\/\/\/\/\/\/\/\/\/\/\/
Do we need to explain the obvious fact that every mathematical problem requires using
the relevant units of measurement?
In this problem we operate with equivalence classes (residues), these classes are from
{0 mod 8} to {7 mod 8}.
Therefore, references to numbers greater than 8 are inappropriate and only show/demonstrate
the general mathematical illiteracy of the person who compiled this problem.
Question 1207685: The inverse of $a$ modulo $44$ is $b$. What is the inverse of $9$ modulo $10$?
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The inverse of a modulo 44 is b. What is the inverse of 9 modulo 10?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Inverse of 9 modulo 10 is an integer number 1 <= n <= 9 such that the product
n*9 is equal to 1 modulo 10.
As soon as you pronounce these words mentally (as the definition), the answer just should be in your mind:
+-----------------------------------------------------------+
| the inverse of 9 modulo 10 is the number 9 modulo 10. |
+-----------------------------------------------------------+
Indeed, 9*9 = 81, which is equal to 1 modulo 10.
ANSWER. The inverse of 9 modulo 10 is the number 9 modulo 10.
Solved.
=================
This problem consists of two statements.
Of these two statements, the first one does not bring any relevant information;
therefore, having sanity in the skull, we should ignore this first statement
(by pointing that it is non-sensical).
The second statement brings the question and makes sense (even if consider it
independently of the first statement).
So, I ignore first statement (as if it is empty and as if it does not exist)
and react to the second statement - it is precisely what I do.
************************************************
In this problem formulation, the first statement
does not carry any information, is not necessary
and interferes with understanding the rest of the task.
************************************************
Question 1207686: Let $x$ and $y$ be integers. If $x$ and $y$ satisfy $41x + 5y = 31$, then find the residue of $x$ modulo $5$.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x and y be integers. If x and y satisfy 41x + 5y = 31, then find the residue of x modulo 5.
~~~~~~~~~~~~~~~~~~~
You are given this equation
41x + 5y = 31, (1)
where x and y are integers. Hence
41x = 31 - 5y. (2)
They want you find residue {x mod 5} from modular equation (2).
It means that you consider equation (2) as an equivalence by modulo 5.
If so, you may forget about the term -5y, because it is 0 (zero) by the modulo 5.
So, your task is to find the residue {x mod 5} from the modular equation
41x = 31 mod 5,
which is equivalent to
41x = 1 mod 5. (3)
The set of possible solutions is x = {0 mod 5}, {1 mod 5}, {2 mod 5}, {3 mod 5} and {4 mod 5}.
x = {0 mod 5} turns (3) into 41*0 = 1 mod 5, which is obviously wrong.
x = {1 mod 5} turns (3) into 41*1 = 1 mod 5, which is obviously correct modular equation ( since 41 mod 5 = 1 mod 5).
x = {2 mod 5} turns (3) into 41*2 = 1 mod 5, which is obviously wrong.
x = {3 mod 5} turns (3) into 41*3 = 1 mod 5, which is obviously wrong.
x = {4 mod 5} turns (3) into 41*4 = 1 mod 5, which is obviously wrong.
Thus of five possible solutions only one is valid: x = {1 mod 5}. ANSWER
So, in this problem, you can easily find the answer by the brute force method.
The problem can be solved using more refined methods, but this reasoning is the number 1,
which you should know and understand as a basic method to start thinking.
Question 1207682: For a certain positive integer $n$, the number $n^{6873}$ leaves a remainder of $3$ when divided by $131.$ What remainder does $n$ leave when divided by $131$?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 75
Explanation
We wish to solve an equation of the form
x^k = b (mod n)
for variable x.
To do so, we'll need Euler's totient function.
phi(n) = Euler's totient of n
phi(n) = the number of integers smaller than n that are relatively prime to n.
Examples:
phi(4) = 2 since set S = {1,3} represent values relatively prime to 4 and there are 2 items inside set S.
and
phi(9) = 6 since set S = {1,2,4,5,7,8} represent values relatively prime to 9 and there are 6 items inside set S.
If n is prime, then phi(n) = n-1
Normally the notation is phi(p) = p-1 for some prime p, but I'll stick to n.
In this case 131 is prime which you can check with a list of primes or a computer program/calculator.
So,
phi(131) = 131-1 = 130
k = 6873
b = 3
n = 131
phi(n) = phi(131) = 130
gcd(b,n) = gcd(3,131) = 1
gcd(k,phi(n)) = gcd(6873,130) = 1
The first gcd equation mentioned above is fairly obvious since 3 is not a factor of the prime 131.
Furthermore note how the digits of 131 do not add to a multiple of 3.
The second gcd equation may not be so obvious. Use the Euclidean Algorithm to determine that value. Various online calculators can show the step-by-step process.
Since both gcd(b,n) and gcd(k,phi(n)) are equal to 1, this means we can proceed with the next set of steps below.
If either expression wasn't 1, then we'd have to find another pathway.
----------------------------
Suppose that
x = b^u
is the solution we're after. The goal is to find the value of u.
Apply substitution:
x^k = b (mod n)
(b^u)^k = b (mod n)
b^(uk) = b (mod n)
b^(uk)*b^(-1) = b*b^(-1) (mod n)
b^(uk-1) = 1 (mod n) ............ Let's call this equation (1)
Now we'll apply Euler's Theorem
b^( phi(n) ) = 1 (mod n)
( b^( phi(n) ) )^c = 1^c (mod n)
b^( phi(n)*c ) = 1 (mod n) ............ Let's call this equation (2)
The left hand sides of equations (1) and (2) can be matched up since the right hand sides are both 1.
Furthermore, the exponents match up to show
uk-1 = phi(n)*c
but this is equivalent to saying
uk = 1 ( mod phi(n) )
----------------------------
To recap, we started at the hypothetical endpoint and made up a wish list in saying the solution is of the form x = b^u
Using that and Euler's Theorem we generated these key equations
b^(uk-1) = 1 (mod n)
and
b^( phi(n)*c ) = 1 (mod n)
Then a bit of steps later we arrive at this
uk = 1 ( mod phi(n) )
Then,
uk = 1 ( mod phi(n) )
6873u = 1 ( mod 130)
113u = 1 ( mod 130)
Notice how 6873 = 113 (mod 130)
This is because both 6873 and 113 give the same remainder when dividing by 130.
In other words, 130d = 6873-113 for some integer value of d
--------------------------------------------------------------------------
Now to solve 113u = 1 ( mod 130)
But 113 isn't too far from 130
113 = -17 (mod 130)
113u = 1 (mod 130)
-17u = 1 (mod 130)
That's equivalent to
-17u-1 = 130c
130c+17u = -1
Use the Euclidean Algorithm and back-substitution to determine that one integer solution is: c = -14, u = 107
I'll skip showing steps since various online calculators can show them. This current solution page is getting fairly lengthy as it is.
We go from
130c+17u = -1
to
130*(-14) + 17*(107) = -1
So,
x = b^u (mod 131)
x = 3^107 (mod 131)
x = 75 (mod 131)
How did I jump from 3^107 (mod 131) to 75 (mod 131) ?
Refer to this lesson about Successive Squaring
That lesson in itself is a bit lengthy, but not too bad once you get enough practice at it.
The answer is 75
I used various software tools to verify that the answer is correct.
One quick tool you can use is WolframAlpha
https://www.wolframalpha.com/input?i=3%5E107+%3D+75+%28mod+131%29
and
https://www.wolframalpha.com/input?i=75%5E6873+mod+131
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For a certain positive integer $n$, the number $n^{6873}$ leaves a remainder of
$3$ when divided by $131.$ What remainder does $n$ leave when divided by $131$?
~~~~~~~~~~~~~~~~~~~~~~~~~~
After seeing the post by @math_tutor, I found some errors in my previous version
that should be fixed. I fixed them, and now you see my updated version.
Now there is no difference between our final numbers/answers.
We are given that the remainder
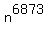 mod 131 is 3.
Notice that 131 is a prime number and 6873 = 113 mod 130.
Now apply the little Fermat's theorem.
It says that for fixed integer "n", where n is relatively prime to 131, the sequence
k --> mod 131 is 3.
Notice that 131 is a prime number and 6873 = 113 mod 130.
Now apply the little Fermat's theorem.
It says that for fixed integer "n", where n is relatively prime to 131, the sequence
k --> 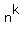 mod 131 is periodical (= cyclic) over integer values k = 1, 2, 3, . . .
with the period of 130.
It tells us that mod 131 is periodical (= cyclic) over integer values k = 1, 2, 3, . . .
with the period of 130.
It tells us that 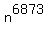 = = 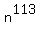 = 3 mod 131.
Based on this information, we should find {n mod 131}.
Let me repeat it again:
Using the little Fermat's theorem, we deduced
from the given info that = 3 mod 131.
Based on this information, we should find {n mod 131}.
Let me repeat it again:
Using the little Fermat's theorem, we deduced
from the given info that 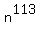 = 3 mod 131.
Having it, we want to find {n mod 131}.
Take = 3 mod 131.
Having it, we want to find {n mod 131}.
Take 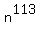 = 3 mod 131 and square it. You will get = 3 mod 131 and square it. You will get 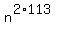 = =  mod 131.
Take mod 131.
Take 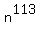 = 3 mod 131 and cube it. You will get = 3 mod 131 and cube it. You will get  = =  mod 131.
. . . and so on . . .
Take mod 131.
. . . and so on . . .
Take 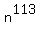 = 3 mod 131 and raise to degree m. You will get = 3 mod 131 and raise to degree m. You will get  = =  mod 131.
The idea is to find a degree m such that m*113 = 1 mod 130.
Then, due to little Fermat's theorem (again) we will have n = mod 131.
The idea is to find a degree m such that m*113 = 1 mod 130.
Then, due to little Fermat's theorem (again) we will have n =  mod 131 and will solve our problem this way.
Thus, our task is to find m, which is
the Modular Multiplicative Inverse to 113 modulo 130.
Fortunately, in the Internet there are calculators for it,
that solve this intermediate task. See these links
Modular Multiplicative Inverse Calculator
https://planetcalc.com/3311/
Inverse Modulo Calculator
https://www.omnicalculator.com/math/inverse-modulo
The Modular Multiplicative Inverse to 113 modulo 130 is 107 modulo 130.
Now the only thing to complete the solution is to find mod 131 and will solve our problem this way.
Thus, our task is to find m, which is
the Modular Multiplicative Inverse to 113 modulo 130.
Fortunately, in the Internet there are calculators for it,
that solve this intermediate task. See these links
Modular Multiplicative Inverse Calculator
https://planetcalc.com/3311/
Inverse Modulo Calculator
https://www.omnicalculator.com/math/inverse-modulo
The Modular Multiplicative Inverse to 113 modulo 130 is 107 modulo 130.
Now the only thing to complete the solution is to find 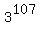 mod 131.
For it, I created Excel spreadsheet below.
The working formula in my spreadsheet is mod 131.
For it, I created Excel spreadsheet below.
The working formula in my spreadsheet is  = =  , ,  = 3.
T A B L E
k = 3.
T A B L E
k 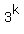 mod 131
------------------------------------
1 3
2 9
3 27
4 81
5 112
6 74
7 91
8 11
9 33
10 99
11 35
12 105
13 53
14 28
15 84
16 121
17 101
18 41
19 123
20 107
21 59
22 46
23 7
24 21
25 63
26 58
27 43
28 129
29 125
30 113
31 77
32 100
33 38
34 114
35 80
36 109
37 65
38 64
39 61
40 52
41 25
42 75
43 94
44 20
45 60
46 49
47 16
48 48
49 13
50 39
51 117
52 89
53 5
54 15
55 45
56 4
57 12
58 36
59 108
60 62
61 55
62 34
63 102
64 44
65 1
66 3
67 9
68 27
69 81
70 112
71 74
72 91
73 11
74 33
75 99
76 35
77 105
78 53
79 28
80 84
81 121
82 101
83 41
84 123
85 107
86 59
87 46
88 7
89 21
90 63
91 58
92 43
93 129
94 125
95 113
96 77
97 100
98 38
99 114
100 80
101 109
102 65
103 64
104 61
105 52
106 25
107 75 <---===
The ANSWER to the problem's question is 75.
In other words, n leaves the remainder 75 when is divided by 131. mod 131
------------------------------------
1 3
2 9
3 27
4 81
5 112
6 74
7 91
8 11
9 33
10 99
11 35
12 105
13 53
14 28
15 84
16 121
17 101
18 41
19 123
20 107
21 59
22 46
23 7
24 21
25 63
26 58
27 43
28 129
29 125
30 113
31 77
32 100
33 38
34 114
35 80
36 109
37 65
38 64
39 61
40 52
41 25
42 75
43 94
44 20
45 60
46 49
47 16
48 48
49 13
50 39
51 117
52 89
53 5
54 15
55 45
56 4
57 12
58 36
59 108
60 62
61 55
62 34
63 102
64 44
65 1
66 3
67 9
68 27
69 81
70 112
71 74
72 91
73 11
74 33
75 99
76 35
77 105
78 53
79 28
80 84
81 121
82 101
83 41
84 123
85 107
86 59
87 46
88 7
89 21
90 63
91 58
92 43
93 129
94 125
95 113
96 77
97 100
98 38
99 114
100 80
101 109
102 65
103 64
104 61
105 52
106 25
107 75 <---===
The ANSWER to the problem's question is 75.
In other words, n leaves the remainder 75 when is divided by 131.
Solved.
------------------
Couple of post-solution notes:
(1) Finding the Modular Multiplicative Inverse to 61 modulo 131 is a technical issue.
I used and referred to online calculators with the only goal do not distract
a reader from the mainstream idea of the solution.
(2) The method making calculations in the spreadsheet is to avoid overflowing (= loosing the precision)
when using direct formula for ( mod 131). mod 131).
Question 1207683: Let $p$ be a prime. What are the possible remainders when $p$ is divided by $17?$ Select all that apply.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Possible remainders are integers from 0 through 16, inclusive:
P = Q x 17 + R
------------------
17 = 1 x 17 + 0
103 = 6 x 17 + 1
2 = 0 x 17 + 2
3 = 0 x 17 + 3
89 = 5 x 17 + 4
5 = 0 x 17 + 5
193 = 11 x 17 + 6
7 = 0 x 17 + 7
59 = 3 x 17 + 8
179 = 10 x 17 + 9
61 = 3 x 17 + 10
11 = 0 x 17 + 11
29 = 1 x 17 + 12
13 = 0 x 17 + 13
31 = 1 x 17 + 14
83 = 4 x 17 + 15
67 = 3 x 17 + 16
This might make you wonder if this is true:
For any prime t and any integer r, 0 < r < t-1,
there will always be a prime p such that when
p is divided by t, the remainder will be r.
We just proved it true for t=17.
Edwin
Question 1207676: Find the remainder when 40^{13} is divided by 81.
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the remainder when 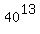 is divided by 81. is divided by 81.
~~~~~~~~~~~~~~~~~~~
It is clear that the mathematical meaning of this problem is not to follow literally
the written formula.
Its meaning is to decrease / (to reduce) the degrees and values of participating numbers
to make calculations easier using standard properties of operations of modular arithmetic.
Following this idea, I write 40 = 36 + 4,
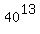 = = 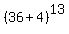 .
Next we should apply the Newtonian binomial formula.
It will give the sum of the terms .
Next we should apply the Newtonian binomial formula.
It will give the sum of the terms 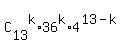 , k = 0, 1, 2, 3, . . . , 13.
All the terms with k >= 2 will be zero by modulo 81, since 36 = 9*4.
Therefore, we can exclude all these terms from our consideration.
So, the terms under our consideration are the terms with k= 0 and k= 1, or , k = 0, 1, 2, 3, . . . , 13.
All the terms with k >= 2 will be zero by modulo 81, since 36 = 9*4.
Therefore, we can exclude all these terms from our consideration.
So, the terms under our consideration are the terms with k= 0 and k= 1, or
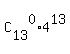 + + 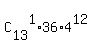 = =  + + 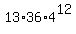 .
This expression is easy to calculate using a regular calculator or Excel spreadsheet;
its value is 7918845952.
Finally, 7918845952 mod 81 is 22 (use long division or Excel function mod)
So, the ANSWER is 22. .
This expression is easy to calculate using a regular calculator or Excel spreadsheet;
its value is 7918845952.
Finally, 7918845952 mod 81 is 22 (use long division or Excel function mod)
So, the ANSWER is 22.
Solved.
----------------
Throwing pebbles into the water from a bridge, look at the circles
they form; otherwise your exercises will be empty deals.
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1207672: For an integer $n,$ let $f(n)$ be the remainder when $n^8 + n^{16}$ is divided by $5.$ Compute $f(0) + f(1) + f(2) + f(3) + f(4).$
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
For n=0,1,2,3,4 determine the pattern of the powers of n mod 5:
n=0: n to any power is 0; the remainder when divided by 5 is always 0
n=1: n to any power is 1; the remainder when divided by 5 is always 1
n=2: the pattern is 2, 4 (=-1), -2, 1 (cycle length 4)
n=3: the pattern is 3, 9 (=-1), -3, 1 (cycle length 4)
n=4: the pattern is 4 (=-1), 1 (cycle length 2)
f(n) is equal to (n^8+n^16) mod 5.
The lengths of the cycles of the remainders are 1, or 2, or 4; 8 and 16 are both multiples of all of those. So both n^8 mod 5 and n^16 mod 5 will be the last number in the pattern for each value of n.
The last numbers in the patterns are 0 for n=0 and 1 for all other values of n. So
f(0) = 0+0 = 0
f(1) = 1+1 = 2
f(2) = 1+1 = 2
f(3) = 1+1 = 2
f(4) = 1+1 = 2
f(0)+f(1)+f(2)+f(3)+f(4) = 0+2+2+2+2 = 8
ANSWER: 8
Question 1207670: Let $a$ be an integer such that $0 \le a \le 10$ and $a^2 \equiv a \pmod{11}$. If $a \neq 0,$ then find the value of $a$.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
Answer by ikleyn(52780)   (Show Source): (Show Source):
Question 1207671: Find a six-digit multiple of $64$ that consists only of the digits $2$ and $4$.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find a six-digit multiple of 64 that consists only of the digits 2 and 4.
~~~~~~~~~~~~~~~~~~
Notice that 64 =  .
(1) Since the number N is a multiple of 64, it is a multiple of 4, too.
Hence, its two right-most digits constitute the number, multiple of 4.
The only possible two-digit numbers consisting of digits 2 and 4 and multiple of 4 are 24 and 44.
So, the two right-most digits of the number N are "24" or "44".
(2) Since the number N is a multiple of 64, it is a multiple of 8, too.
Hence, its three right-most digits constitute the number, multiple of 8
(according to the rule of divisibility by 8).
In addition, we know that its two right-most digits are "24" or "44".
The only possible such three-digit numbers consisting of digits 2 and 4 and multiple of 8 are 224, 424, 244 and 444.
Of them, only two, namely "224" and "424", are divisible by 8.
So, the three right-most digits of the number N are "224" or "424".
(3) Since the number N is a multiple of 64, it is a multiple of 16, too.
Hence, its four right-most digits constitute the number, multiple of 16
(according to the rule of divisibility by 16).
In addition, we know that its three right-most digits are "224" or "424".
The only possible such four-digit numbers consisting of digits 2 and 4 and multiple of 16 are "2224", "4224", "2424" or "4424".
Of them, only two, namely "2224" and "4224", are divisible by 16.
So, the four right-most digits of the number N are "2224" or "4224".
(4) Since the number N is a multiple of 64, it is a multiple of 32, too.
Hence, its five right-most digits constitute the number, multiple of 32
(according to the rule of divisibility by 32).
In addition, we know that its four right-most digits are "2224" or "4224".
The only possible such five-digit numbers consisting of digits 2 and 4 and multiple of 32 are "22224", "42224", "24224" or "44224".
Of them, only two numbers, namely "24224" and "44224", are divisible by 32.
So, the five right-most digits of the number N are "24224" or "44224".
(5) The number N is a multiple of 64. Hence, it is a multiple of 32, too.
Due to it, we know that its five right-most digits are "24224" or "44224".
The only such six-digit numbers consisting of digits 2 and 4 are "224224", "424224", "244224" or "444224".
Of them, only two are divisible by 64: 244224 and 444224.
So, these two numbers are six-digit numbers satisfying the given condition.
ANSWER. 244224 and 444224 are two six-digit numbers satisfying the given condition.
These two numbers are UNIQUE: there are no other six-digit integer positive numbers satisfying imposed conditions. .
(1) Since the number N is a multiple of 64, it is a multiple of 4, too.
Hence, its two right-most digits constitute the number, multiple of 4.
The only possible two-digit numbers consisting of digits 2 and 4 and multiple of 4 are 24 and 44.
So, the two right-most digits of the number N are "24" or "44".
(2) Since the number N is a multiple of 64, it is a multiple of 8, too.
Hence, its three right-most digits constitute the number, multiple of 8
(according to the rule of divisibility by 8).
In addition, we know that its two right-most digits are "24" or "44".
The only possible such three-digit numbers consisting of digits 2 and 4 and multiple of 8 are 224, 424, 244 and 444.
Of them, only two, namely "224" and "424", are divisible by 8.
So, the three right-most digits of the number N are "224" or "424".
(3) Since the number N is a multiple of 64, it is a multiple of 16, too.
Hence, its four right-most digits constitute the number, multiple of 16
(according to the rule of divisibility by 16).
In addition, we know that its three right-most digits are "224" or "424".
The only possible such four-digit numbers consisting of digits 2 and 4 and multiple of 16 are "2224", "4224", "2424" or "4424".
Of them, only two, namely "2224" and "4224", are divisible by 16.
So, the four right-most digits of the number N are "2224" or "4224".
(4) Since the number N is a multiple of 64, it is a multiple of 32, too.
Hence, its five right-most digits constitute the number, multiple of 32
(according to the rule of divisibility by 32).
In addition, we know that its four right-most digits are "2224" or "4224".
The only possible such five-digit numbers consisting of digits 2 and 4 and multiple of 32 are "22224", "42224", "24224" or "44224".
Of them, only two numbers, namely "24224" and "44224", are divisible by 32.
So, the five right-most digits of the number N are "24224" or "44224".
(5) The number N is a multiple of 64. Hence, it is a multiple of 32, too.
Due to it, we know that its five right-most digits are "24224" or "44224".
The only such six-digit numbers consisting of digits 2 and 4 are "224224", "424224", "244224" or "444224".
Of them, only two are divisible by 64: 244224 and 444224.
So, these two numbers are six-digit numbers satisfying the given condition.
ANSWER. 244224 and 444224 are two six-digit numbers satisfying the given condition.
These two numbers are UNIQUE: there are no other six-digit integer positive numbers satisfying imposed conditions.
Solved.
Question 1207654: A positive integer is called terrific if it has exactly $3$ positive divisors.
What is the smallest number of primes that could divide a terrific positive integer?
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
You can put this solution on YOUR website! If the three divisors must be the smallest and they be prime numbers, then 
I assumed each divisor should be none the same which may be incorrect.
Question 1207656: A positive integer is called terrific if it has exactly $3$ positive divisors.
What is the smallest terrific positive integer?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A positive integer has exactly 3 positive divisors if and only if its prime factorization is p^2, where p is a prime number.
The smallest positive integer with exactly 3 positive divisors is p^2, where p is the smallest prime number. The smallest prime number is 2, so the smallest positive integer with exactly 3 positive divisors is 2^2 = 4.
ANSWER: 4
Question 1207657: The number $100$ has four perfect square divisors, namely $1,$ $4,$ $25,$ and $100.$
What is the smallest positive integer that has exactly $2$ perfect square divisors?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The two smallest perfect squares are 1 and 4, so the smallest positive integer that has exactly 2 perfect square divisors is the least common multiple of 1 and 4, which is, trivially, 4.
ANSWER: 4
Question 1207613: For a positive integer $n$, $\phi(n)$ denotes the number of positive integers less than or equal to $n$ that are relatively prime to $n$.
What is $\phi(5)$?
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 4
Explanation
For any prime p, we have the following:
phi(p) = p-1
There are p-1 positive integers smaller than p that are relatively prime to p.
1, 2, 3, ..., p-2, p-1
This intuitively makes sense because all of these values are not factors of the prime p (well except for the trivial case 1)
Examples:
phi(7) = 6
phi(11) = 10
If we had some value not relatively prime to p, smaller than p, then it would mean p isn't prime.
For instance if 2 and p weren't relatively prime, then p = 2k and p is even. But at this point p is not prime.
Further Reading
https://mathworld.wolfram.com/TotientFunction.html
and
https://en.wikipedia.org/wiki/Euler%27s_totient_function
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295
|


