This Lesson (Why 3^n + 7^n - 2 is divisible by 8 for all positive integer n ?) was created by by ikleyn(52906)   : View Source, ShowAbout ikleyn:
Why 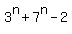 is divisible by 8 for all positive integer n ? is divisible by 8 for all positive integer n ?
Problem 1Show that 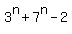 is divisible by 8 for all positive integers n. is divisible by 8 for all positive integers n.
Solution
Make a table for degrees 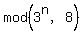 , , 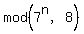 and the expression and the expression 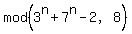 , as shown below.
n , as shown below.
n 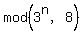 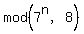 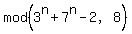 -------------------------------------------------------------------
1 3 7 8
2 1 1 0
3 3 7 8
4 1 1 0
5 3 7 8
6 1 1 0
7 3 7 8
8 1 1 0
9 3 7 8
10 1 1 0
From this table, you see that the sequence
-------------------------------------------------------------------
1 3 7 8
2 1 1 0
3 3 7 8
4 1 1 0
5 3 7 8
6 1 1 0
7 3 7 8
8 1 1 0
9 3 7 8
10 1 1 0
From this table, you see that the sequence 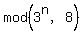 is cyclic with the cycle length of 2.
It is easy to understand, because 3^2 = 9 is 1 modulo 8; so, multiplication by 3^2 keeps the value modulo 8 THE SAME.
Therefore, the remainder is cyclic with the cycle length of 2.
It is easy to understand, because 3^2 = 9 is 1 modulo 8; so, multiplication by 3^2 keeps the value modulo 8 THE SAME.
Therefore, the remainder 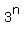 modulo 8 is cyclic with the period 2.
Similarly, from the table, you see that the sequence modulo 8 is cyclic with the period 2.
Similarly, from the table, you see that the sequence 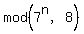 is cyclic with the cycle length of 2.
It is easy to understand, too, because 7^2 = 49 is 1 modulo 8; so, multiplication by 7^2 keeps the value modulo 8 THE SAME.
Therefore, if the remainder is cyclic with the cycle length of 2.
It is easy to understand, too, because 7^2 = 49 is 1 modulo 8; so, multiplication by 7^2 keeps the value modulo 8 THE SAME.
Therefore, if the remainder 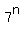 modulo 8 is is cyclic with the period 2.
After that, it is clear why the expression modulo 8 is is cyclic with the period 2.
After that, it is clear why the expression 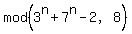 is zero,
and the problem is solved. is zero,
and the problem is solved.
Problem 2Prove that  is divisible by 4 for every natural number n. is divisible by 4 for every natural number n.
Solution
First, notice that 7^n and 3^n give THE SAME REMAINDER when divided by 4.
It is because the difference
7^n - 3^n = (7-3) * (7^(n-1) + 7^(n-2)*3 + 7^(n-3)*3^2 + . . . 7^1*3^(n-2) + 3^(n-1))
is divizible by 7-3 = 4. // Recall the general formula
a^n - b^n = (a-b) * (a^(n-1) + a^(n-2)*b + a^(n-3)*b^2 + . . . a^1*b^(n-2) + b^(n-1)).
Therefore, 6*7^n — 2*3^n gives the same remainder, when divided by 4, as 6*3^n — 2*3^n,
which simply equals to (collect like terms) 4*3^n,
which is, obviously, divisible by 4, since it is a multiple of 4.
At this point, the statement is proved and the problem is solved, in full.
My other lessons in this site on miscellaneous problems on divisibility of integer numbers are
- Light flashes on a Christmas tree and a Least Common Multiple
- The number that leaves a remainder 1 when divided by 2, by 3, by 4, by 5 and so on until 9
- The number which gives remainder 4 when divided by 7, remainder 5 when divided by 8 and remainder 6 when divided by 9
- Introductory problems on divisibility of integer numbers
- Finding Greatest Common Divisor of integer numbers
- Relatively prime numbers help to solve the problem
- Solving equations in integer numbers
- Quadratic polynomial with odd integer coefficients can not have a rational root
- Proving an equation has no integer solutions
- Composite number of the form (4n+3) must have a prime divisor of the form (4n+3)
- Problems on divisors of a given number
- How many three-digit numbers are multiples of both 5 and 7?
- How many 3-digit numbers are not divisible by 2; not divisible by 3; not divisible by either 2 or 3
- How many integer numbers in the range 1-300 are divisible by at least one of the integers 4, 6 and 15 ?
- Find the remainder of division
- What is the last digit of the number a^n ?
- Find the last three digits of these numbers
- Find the last two digits of the number 3^123 + 7^123 + 9^123
- Find the last two digits of (1! + 2! + 3! + ... + 2024!)^2024
- Find n-th term of a sequence
- Solving Diophantine equations
- How many integers of the form n^2 + 18n + 13 are perfect squares
- Miscellaneous problems on divisibility numbers
- Find the sum of digits of integer numbers
- Two-digit numbers with digit "9"
- Find a triangle with integer side lengths and integer area
- Math circle level problem on the hundred-handed monster Briareus
- Math Circle level problem on lockers and divisors of integer numbers
- Nice entertainment problems related to divisibility properties
- Solving problems on modular arithmetic
- Using the little Fermat's theorem to solve a problem on modular arithmetic
- OVERVIEW of miscellaneous solved problems on divisibility of integer numbers
This lesson has been accessed 995 times.
|

