Proving an equation has no integer solutions
Problem 1
Prove that the equation 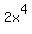 +
+ 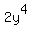 =
=  has no solutions in integer numbers.
has no solutions in integer numbers.
Solution
I will prove it in 3 (three) steps.
Step 1. Lemma
STATEMENT:
If 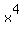 +
+ 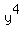 =
= 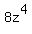 where x, y and z are integer numbers, then both x and y are even numbers.
PROOF of the statement.
For the proof, present x = 8m + i, y = 8n + j, where 0 <= i <=7, 0 <= j <= 7.
Then write
where x, y and z are integer numbers, then both x and y are even numbers.
PROOF of the statement.
For the proof, present x = 8m + i, y = 8n + j, where 0 <= i <=7, 0 <= j <= 7.
Then write
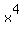 +
+ 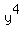 =
= 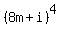 +
+ 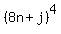 = (use the binomial formula) = (sum of the terms multiple of 8) +
= (use the binomial formula) = (sum of the terms multiple of 8) +  +
+  .
Below I prepared a rectangular table containing the numbers
.
Below I prepared a rectangular table containing the numbers 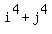 mod 8 with two entries
mod 8 with two entries  and
and  The table has two entries columns at the left and two entries rows at the top:
1 2 3 4 5 6 7 <<< j
i i^4 mod 8 1 0 1 0 1 0 1 <<< j^4 mod 8
1 1 2 1 2 1 2 1 2
2 0 1 0 1 0 1 0 1
3 1 2 1 2 1 2 1 2
4 0 1 0 1 0 1 0 1
5 1 2 1 2 1 2 1 2
6 0 1 0 1 0 1 0 1
7 1 2 1 2 1 2 1 2
The most left column simply lists the numbers (remainders) i = 1, 2, 3, 4, 5 , 6, 7 (mod 8).
The next column contains the number (remainders)
The table has two entries columns at the left and two entries rows at the top:
1 2 3 4 5 6 7 <<< j
i i^4 mod 8 1 0 1 0 1 0 1 <<< j^4 mod 8
1 1 2 1 2 1 2 1 2
2 0 1 0 1 0 1 0 1
3 1 2 1 2 1 2 1 2
4 0 1 0 1 0 1 0 1
5 1 2 1 2 1 2 1 2
6 0 1 0 1 0 1 0 1
7 1 2 1 2 1 2 1 2
The most left column simply lists the numbers (remainders) i = 1, 2, 3, 4, 5 , 6, 7 (mod 8).
The next column contains the number (remainders)  mod 8.
The most upper row lists the numbers (remainders) j = 1, 2, 3, 4, 5 , 6, 7 (mod 8).
The second row contains the number (remainders)
mod 8.
The most upper row lists the numbers (remainders) j = 1, 2, 3, 4, 5 , 6, 7 (mod 8).
The second row contains the number (remainders)  mod 8.
The table itself contains, as I just said, the sums
mod 8.
The table itself contains, as I just said, the sums 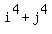 mod 8.
From the table you can see that
mod 8.
From the table you can see that 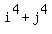 is multiple of 8 if and only if BOTH i and j are EVEN numbers.
(Then and only then we have 0 (zero) in the Table).
Thus the lemma is proved.
is multiple of 8 if and only if BOTH i and j are EVEN numbers.
(Then and only then we have 0 (zero) in the Table).
Thus the lemma is proved.
Step 2. (To warm your mind)
Let integer numbers x, y and z are the solution to the given equation:
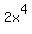 +
+ 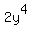 =
=  .
Then the left side is an even number.
Hence, right side is an even number.
Then
.
Then the left side is an even number.
Hence, right side is an even number.
Then  is an even number.
It implies that z itself is an even number: z =
is an even number.
It implies that z itself is an even number: z = 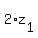 , where
, where 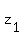 is integer.
Then the given equation can be written in the form
is integer.
Then the given equation can be written in the form
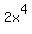 +
+ 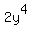 =
= 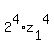 .
Reduce/(cancel) the factor 2 in both sides. You will get
.
Reduce/(cancel) the factor 2 in both sides. You will get
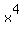 +
+ 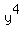 =
= 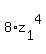 .
Now, according to the lemma, both x and y are even numbers.
This chain of arguments opens the way for the "infinite descent" method.
(The method is attributed to Pierre Fermat and was used by Leonard Euler).
.
Now, according to the lemma, both x and y are even numbers.
This chain of arguments opens the way for the "infinite descent" method.
(The method is attributed to Pierre Fermat and was used by Leonard Euler).
Step 3. (Formal proof)
Let assume that equation
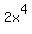 +
+ 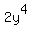 =
=  (1)
has the solution in integer numbers and let the triple (x,y,z) be the solution.
It is clear that if all three numbers x, y and z are even, we can cancel all the three numbers by this common divisor 2,
and the new triple also will be the solution to the same equation.
We will cancel this common divisor 2 as many times as possible.
Finally, we can assume that we got (we have) the triple, in which NO MORE THAN ONE member of "x" and "y" is multiple of 2.
(If BOTH "x" AND "y" ARE multiples of 2, then obviously the third number z is also multiple of 2 - the case which we just EXCLUDED).
OK. So, let us assume first that no one of the three terms x, y, z is multiple of 2.
In the equation (1), the left side is an even number.
Hence, right side is an even number.
Then
(1)
has the solution in integer numbers and let the triple (x,y,z) be the solution.
It is clear that if all three numbers x, y and z are even, we can cancel all the three numbers by this common divisor 2,
and the new triple also will be the solution to the same equation.
We will cancel this common divisor 2 as many times as possible.
Finally, we can assume that we got (we have) the triple, in which NO MORE THAN ONE member of "x" and "y" is multiple of 2.
(If BOTH "x" AND "y" ARE multiples of 2, then obviously the third number z is also multiple of 2 - the case which we just EXCLUDED).
OK. So, let us assume first that no one of the three terms x, y, z is multiple of 2.
In the equation (1), the left side is an even number.
Hence, right side is an even number.
Then  is an even number.
It implies that z itself is an even number: z =
is an even number.
It implies that z itself is an even number: z = 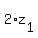 , where
, where 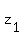 is integer.
Then the given equation can be written in the form
is integer.
Then the given equation can be written in the form
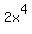 +
+ 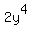 =
= 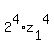 .
Reduce/(cancel) the factor 2 in both sides. You will get
.
Reduce/(cancel) the factor 2 in both sides. You will get
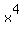 +
+ 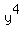 =
= 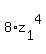 .
But the LEMMA IMPLIES that BOTH x and y are even numbers.
CONTRADICTION.
OK. So, let us assume next that only one of the two terms "x" and "y" is multiple of 2.
In the equation (1), the left side is an even number.
Hence, right side is an even number.
Then
.
But the LEMMA IMPLIES that BOTH x and y are even numbers.
CONTRADICTION.
OK. So, let us assume next that only one of the two terms "x" and "y" is multiple of 2.
In the equation (1), the left side is an even number.
Hence, right side is an even number.
Then  is an even number.
It implies that z itself is an even number: z =
is an even number.
It implies that z itself is an even number: z = 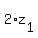 , where
, where 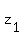 is integer.
Then the given equation can be written in the form
is integer.
Then the given equation can be written in the form
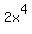 +
+ 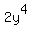 =
= 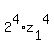 .
Reduce/(cancel) the factor 2 in both sides. You will get
.
Reduce/(cancel) the factor 2 in both sides. You will get
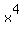 +
+ 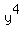 =
= 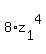 .
But the LEMMA IMPLIES that BOTH x and y are even numbers.
CONTRADICTION.
.
But the LEMMA IMPLIES that BOTH x and y are even numbers.
CONTRADICTION.
These contradictions prove that our starting assumption that the given equation has the solutions in integer numbers was wrong.
The proof is completed and the problem is solved.
My other lessons in this site on miscellaneous problems on divisibility of integer numbers are
- Light flashes on a Christmas tree and a Least Common Multiple
- The number that leaves a remainder 1 when divided by 2, by 3, by 4, by 5 and so on until 9
- The number which gives remainder 4 when divided by 7, remainder 5 when divided by 8 and remainder 6 when divided by 9
- Introductory problems on divisibility of integer numbers
- Finding Greatest Common Divisor of integer numbers
- Relatively prime numbers help to solve the problem
- Quadratic polynomial with odd integer coefficients can not have a rational root
- Composite number of the form (4n+3) must have a prime divisor of the form (4n+3)
- Problems on divisors of a given number
- How many three-digit numbers are multiples of both 5 and 7?
- How many 3-digit numbers are not divisible by 2; not divisible by 3; not divisible by either 2 or 3
- How many integer numbers in the range 1-300 are divisible by at least one of the integers 4, 6 and 15 ?
- Find the remainder of division
- Why 3^n + 7^n - 2 is divisible by 8 for all positive integer n ?
- What is the last digit of the number a^n ?
- Find the last three digits of these numbers
- Find the last two digits of the number 3^123 + 7^123 + 9^123
- Find the last two digits of (1! + 2! + 3! + ... + 2024!)^2024
- Find n-th term of a sequence
- Solving Diophantine equations
- How many integers of the form n^2 + 18n + 13 are perfect squares
- Miscellaneous problems on divisibility numbers
- Find the sum of digits of integer numbers
- Two-digit numbers with digit "9"
- Find a triangle with integer side lengths and integer area
- Math circle level problem on the hundred-handed monster Briareus
- Math Circle level problem on lockers and divisors of integer numbers
- Nice entertainment problems related to divisibility property
- Solving problems on modular arithmetic
- Using the little Fermat's theorem to solve a problem on modular arithmetic
- OVERVIEW of miscellaneous solved problems on divisibility of integer numbers

