Question 977111: show that square of every positive integer takes any one of the form 3p or 3p+1?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A positive integer, when divided by 3, can divide evenly, or have a remainder of 1, or have a remainder of 2.
It must be one of those 3 cases; there is no other possibility.
So, a positive integer can be
a multiple of 3, of the form 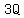 , or , or
be of the form 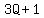 (if it has a remainder of 1 when divided by 3), or (if it has a remainder of 1 when divided by 3), or
be of the form 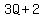 (if it has a remainder of 2 when divided by 3), (if it has a remainder of 2 when divided by 3),
with  being a non-negative integer in each case. being a non-negative integer in each case.
The square of 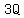 is is  with with  . .
The squares of 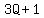 and and 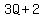 can be calculated as the square of a binomial with a formula proven in algebra class: can be calculated as the square of a binomial with a formula proven in algebra class:
 . .
The square of 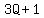 is is  with with  . .
The square of 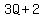 is is  with with  . .
In other words, when divided by 3, the square of an integer can
divide evenly,
or leave a remainder of 1.
There is no other possibility.
|
|
|