SOLUTION: Prove if {{{a/b = c/d = (a - c)/(b - d)}}} It's just like {{{2/4 = 1/2 = (2 - 1)/(4-2)}}}

We need to prove that if any 2 of these

, , and 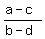 are equal, they are also
equal to the third one:

1. Prove that if , then 



Cross-multiply



Multiply both sides by -1



Add ab to both sides



Factor out a on the left.
Factor out b on the right.



Divide both sides by 

  

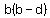
Cancel:



, and since ,



2. Prove that if , then 



Cross-multiply





Since ab=ba,



Subtract ab from both sides



Multiply through by -1



Divide through by bd



Cancel



, therefore



3. Prove that if , then 



Cross-multiply





Since cd=dc,



Add cd to both sides



Divide through by bd



Cancel



, therefore



Edwin