Question 847901: Find the least number which when divided by 6, 8, and 15 leaves a remainder 5, but when divided by 13, leaves no remainder.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the least number which when divided by 6, 8, and 15 leaves a remainder 5, but when divided by 13, leaves no remainder.
Let the number be N
N is 5 more than a multiple of 6, so N=6p+5 for some integer p.
N is 5 more than a multiple of 8, so N=8q+5 for some integer q.
N is 5 more than a multiple of 15, so N=15r+5 for some integer r.
N is a multiple of 13, so N=13t
So
(1) N = 6p+5 = 8q+5 = 15r+5 = 13t
Since N = 15r+5 = 5(3r+1), is a multiple of 13, 3r+1 is also multiple of 13.
So 3r+1 = 13u for some integer u
3r = 13u-1
So 15r = 65u-5
So (1) becomes
N = 6p+5 = 8q+5 = 65u-5+5 = 13t
N = 6p+5 = 8q+5 = 65u = 13t
We can dispense with the 13t, since N is a multiple of 65, it's
automatically a multiple of 13. So (1) becomes
(2) N = 6p+5 = 8q+5 = 65u
Since 6p+5 = 8q+5
6p = 8q
3p = 4q
Write 4q as 3q+q
3p = 3q+q
Divide through by 3
p = q+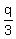 So p-q =
So p-q = 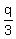 Since p-q is an integer, so is
Since p-q is an integer, so is 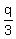 , say the integer v
Then p-q = v and , say the integer v
Then p-q = v and 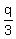 = v
So = v
So 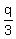 = v
q = 3v
p-q = v
p-3v = v
p = 4v
Substituting in (2)
N = 6(4v)+5 = 8(3v)+5 = 65u
N = 24v+5 = 65u
Since 24v+5 = 65u
24v = 65u-5
24v = 5(13u-1)
v is a multiple of 5, so v = 5w for some integer w
24(5w) = 5(13u-1)
14w = 13u-1
1 = 13u-14w
Write 14 as 13+1
1 = 13u-(13+1)w
1 = 13u-13w-w
Divide through by 13 = v
q = 3v
p-q = v
p-3v = v
p = 4v
Substituting in (2)
N = 6(4v)+5 = 8(3v)+5 = 65u
N = 24v+5 = 65u
Since 24v+5 = 65u
24v = 65u-5
24v = 5(13u-1)
v is a multiple of 5, so v = 5w for some integer w
24(5w) = 5(13u-1)
14w = 13u-1
1 = 13u-14w
Write 14 as 13+1
1 = 13u-(13+1)w
1 = 13u-13w-w
Divide through by 13
 = u-w- = u-w-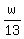
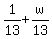 = u-w
The right side is an integer so the left side must be also.
Suppose that integer is x. Then = u-w
The right side is an integer so the left side must be also.
Suppose that integer is x. Then
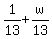 = x and u-w = x
1 + w = 13x
w = 13x-1
Substituting in
u-w = x
u-(13x-1) = x
u-13x+1 = x
u = 14x-1
Since N = 65u
N = 65(14x-1)
N = 910x-65
The smallest value x can take on is 1, so
N = 910(1)-65
N = 910-65
N = 845
Edwin = x and u-w = x
1 + w = 13x
w = 13x-1
Substituting in
u-w = x
u-(13x-1) = x
u-13x+1 = x
u = 14x-1
Since N = 65u
N = 65(14x-1)
N = 910x-65
The smallest value x can take on is 1, so
N = 910(1)-65
N = 910-65
N = 845
Edwin
|
|
|