SOLUTION: Make a conjecture about the following results: Square root of 2 2/3=2 square root of 2/3. Square root of 3 3/8=3 square root of 3/8. Try to prove your conjecture.

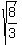
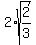
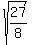
It's easy to see the pattern, except for the denominators, where
I have put question marks below.  There is no way to determine just by
inspection, a sequence for the denominators with just the first 
two terms, 3 and 8.  We could guess a general term for the
denominators, but that would be risky business. 

 

Now let's let D be those denominators, 



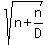
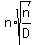and solve for D.  Square both sides:

  



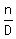
Multiply both sides by D



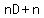
Divide through by n



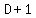
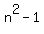 for n > 1

So our conjecture is found by substituting that
expression for D in:



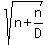
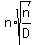
 for n > 1

To prove that we have to show that each side is non-
negative (obvious) and have the same square.  We show 
that each side has the same square:

LEFT SIDE = 

SQUARE OF LEFT SIDE =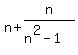 

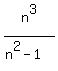RIGHT SIDE = 

SQUARE OF RIGHT SIDE = 

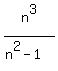So they have the same square and are both non-negative so the conjecture
is proved.

Edwin