 has only the prime divisors
has only the prime divisors  and
and  .
Every divisor of
.
Every divisor of  is therefore of the form
is therefore of the form 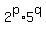 ,
where
,
where  and
and  are elements of {0,1,2,3}. Since there
are
are elements of {0,1,2,3}. Since there
are  choices for
choices for  and
and  choices for
choices for  , there are
, there are  divisors of
divisors of  . That isn't necessary to know. But
in the product of all
. That isn't necessary to know. But
in the product of all  divisors of
divisors of  ,
, 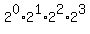 or
or  , and
, and 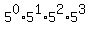 or
or  occur exactly
occur exactly  times each.
Since
times each.
Since  and
and  both occur
both occur  times each in the product
of all divisors, the product of the divisors must be
times each in the product
of all divisors, the product of the divisors must be
 , choice a)
Edwin
, choice a)
Edwin