Question 1175732: How many positive integer factors of 360 are also multiples of 4?
Found 3 solutions by MathLover1, Alan3354, ikleyn:
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!
The factors of  are:
 , , ,  ,  , ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  , ,  , ,  ,  ,
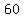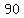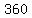
multiples of up to are:
, , , , , ,  ,  , , , ,,,
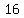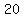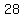How many positive integer factors of are also multiples of ?
answer: there are  positive integer factors of that are also multiples of
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! How many positive integer factors of 360 are also multiples of 4?
-------------
I don't think there's a way to calculate that.
Just list them and count them.
Answer by ikleyn(52802)  (Show Source):
You can put this solution on YOUR website! .
The solution by @MathLover1 is incorrect.
Her answer " 14 " is not correct.
The numbers 16 and 32 of her list are not divisors of 360.
I came to bring the correct solution.
360 = 4*90 = 8*45 = 8*3^2*5 = 4*(2*3^2*5).
All divisors of 360, that are multiples of 4, are the numbers of the primary decomposition  ,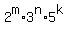
where indexes m, n and k vary independently in their ranges
m = 0, 1 (two values)
n = 0, 1, 2 (three values)
k = 0, 1 (two values).
THEREFORE, the number of all positive divisors of 360, that are multiples of 4 is 2*3*2 = 12. ANSWER
Solved.
----------
If you want to learn on how to calculate the number of divisors d(N) of a given integer number N, look into my lesson
- Problems on divisors of a given number
in this site.
It is one of the basic introductory subjects of the elementary number theory.
|
|
|
