|
Tutors Answer Your Questions about decimal-numbers (FREE)
Question 1206057: Consider a population that grows according to the recursive rule Pn=Pn-1+35, with initial population Po=20.
Then:
P1 = __________
P2 = _________
Find an explicit formula for the population. Your formula should involve n (use lowercase n)
Pn= __________
Use your explicit formula to find P100
P100 =__________
Click here to see answer by ikleyn(52778)   |
Question 1207584: Let $N$ be a positive integer. The number $N$ has three digits when expressed in base $7$. When the number $N$ is expressed in base $12$, it has the same three digits, in reverse order. What is $N$? (Express your answer in decimal.)
Click here to see answer by greenestamps(13198)   |
Question 1207585: What are the first $5$ digits after the decimal point (technically the hexadecimal point...) when the fraction $\frac{2}{17}$ is written in base $16$?
(Express your answer as a five digit hexadecimal number. You do not need to include the subscript to indicate the base.)
Click here to see answer by greenestamps(13198)   |
Question 1207598: When fractions are expressed in different bases, they can be terminating or repeating. For example, when $\frac{1}{5}$ is expressed in base $3,$ the result is
\[0.\overline{0121}_3 = 0.01210121 \dots,\]
which is repeating.
When $\frac{1}{288}$ is expressed in base $13,$ is it terminating or repeating?
Click here to see answer by greenestamps(13198)   |
Question 1207598: When fractions are expressed in different bases, they can be terminating or repeating. For example, when $\frac{1}{5}$ is expressed in base $3,$ the result is
\[0.\overline{0121}_3 = 0.01210121 \dots,\]
which is repeating.
When $\frac{1}{288}$ is expressed in base $13,$ is it terminating or repeating?
Click here to see answer by ikleyn(52778)   |
Question 1207611: When fractions are expressed in different bases, they can be terminating or repeating. For example, when $\frac{1}{5}$ is expressed in base $3,$ the result is
\[0.\overline{0121}_3 = 0.01210121 \dots,\]
which is repeating.
When $\frac{1}{288}$ is expressed in base $35,$ is it terminating or repeating?
Click here to see answer by ikleyn(52778)   |
Question 1207761: A sugar molecule has twice as many atoms of hydrogen as it does oxygen and one more atom of carbon than oxygen. If a sugar molecule has a total of 45 atoms, how many are oxygen? How many are hydrogen?
Let me see.
Atoms = 2x
Hydrogen = x
2x + x = 45
Is this equation correct?
Click here to see answer by mananth(16946)   |
Question 1207761: A sugar molecule has twice as many atoms of hydrogen as it does oxygen and one more atom of carbon than oxygen. If a sugar molecule has a total of 45 atoms, how many are oxygen? How many are hydrogen?
Let me see.
Atoms = 2x
Hydrogen = x
2x + x = 45
Is this equation correct?
Click here to see answer by ikleyn(52778)   |
Question 1207761: A sugar molecule has twice as many atoms of hydrogen as it does oxygen and one more atom of carbon than oxygen. If a sugar molecule has a total of 45 atoms, how many are oxygen? How many are hydrogen?
Let me see.
Atoms = 2x
Hydrogen = x
2x + x = 45
Is this equation correct?
Click here to see answer by josgarithmetic(39617)  |
Question 1207782: 1. Suppose that you have entered an 87-mile biathlon that consists of a run and a bicycle race. During Explaining Concepts:Discussion and Writing your run, your average speed is 6 miles per hour, and during your bicycle race, your average speed is 25 miles per hour. You finish the race in 5 hours. What is the distance of the run? What is the distance of the bicycle race?
2. In the 1984 Olympics, C.Lewis of the United States won the gold medal in the 100-meter race with a time of 9.99 seconds. In the 1896 Olympics,Thomas Burke,also of the United States, won the gold medal in the 100-meter race in 12.0 seconds. If they ran in the same race repeating their respective times, by how many meters would Lewis beat Burke?
Click here to see answer by josgarithmetic(39617)  |
Question 1207782: 1. Suppose that you have entered an 87-mile biathlon that consists of a run and a bicycle race. During Explaining Concepts:Discussion and Writing your run, your average speed is 6 miles per hour, and during your bicycle race, your average speed is 25 miles per hour. You finish the race in 5 hours. What is the distance of the run? What is the distance of the bicycle race?
2. In the 1984 Olympics, C.Lewis of the United States won the gold medal in the 100-meter race with a time of 9.99 seconds. In the 1896 Olympics,Thomas Burke,also of the United States, won the gold medal in the 100-meter race in 12.0 seconds. If they ran in the same race repeating their respective times, by how many meters would Lewis beat Burke?
Click here to see answer by ikleyn(52778)   |
Question 1207782: 1. Suppose that you have entered an 87-mile biathlon that consists of a run and a bicycle race. During Explaining Concepts:Discussion and Writing your run, your average speed is 6 miles per hour, and during your bicycle race, your average speed is 25 miles per hour. You finish the race in 5 hours. What is the distance of the run? What is the distance of the bicycle race?
2. In the 1984 Olympics, C.Lewis of the United States won the gold medal in the 100-meter race with a time of 9.99 seconds. In the 1896 Olympics,Thomas Burke,also of the United States, won the gold medal in the 100-meter race in 12.0 seconds. If they ran in the same race repeating their respective times, by how many meters would Lewis beat Burke?
Click here to see answer by MathTherapy(10551)   |
Question 1207837: Brittany needed new tires for her truck. She went to the auto shop and bought 4 tires on sale for $85.95 each. The salesman told her that she saved a total of $96.16. If Brittany saved the same amount on each tire, what was the original price of each tire?
Click here to see answer by josgarithmetic(39617)  |
Question 1207837: Brittany needed new tires for her truck. She went to the auto shop and bought 4 tires on sale for $85.95 each. The salesman told her that she saved a total of $96.16. If Brittany saved the same amount on each tire, what was the original price of each tire?
Click here to see answer by ikleyn(52778)   |
Question 1207842: Find an equation for the line that is described. Write the answer in the two forms y = mx + b and Ax + By + C = 0.
A. Is parallel to 2x - 5y = 10 and passes through ( 1, 2)
B. Is parallel to 4x + 5y = 20 and passes through (0, 0)
Click here to see answer by greenestamps(13198)   |
Question 1208054: When expanded as a decimal, the fraction 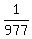 has a repetend (the repeating part of the decimal) that begins right after the decimal point, and is 976 digits long. If the last three digits of the repetend are ABC, compute the digits A, B, and C. has a repetend (the repeating part of the decimal) that begins right after the decimal point, and is 976 digits long. If the last three digits of the repetend are ABC, compute the digits A, B, and C.
A=
B=
C=
Click here to see answer by ikleyn(52778)   |
Question 1208054: When expanded as a decimal, the fraction 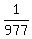 has a repetend (the repeating part of the decimal) that begins right after the decimal point, and is 976 digits long. If the last three digits of the repetend are ABC, compute the digits A, B, and C. has a repetend (the repeating part of the decimal) that begins right after the decimal point, and is 976 digits long. If the last three digits of the repetend are ABC, compute the digits A, B, and C.
A=
B=
C=
Click here to see answer by Edwin McCravy(20054)   |
Question 1208250: The total distance of a family road trip is 668.25 miles. After traveling 50.75 miles, a kid asked how much longer it would take to get there. If the car travels 65 miles every hour, how many hours will it take to finish the trip, if they do not stop?
Click here to see answer by ikleyn(52778)   |
Question 1208250: The total distance of a family road trip is 668.25 miles. After traveling 50.75 miles, a kid asked how much longer it would take to get there. If the car travels 65 miles every hour, how many hours will it take to finish the trip, if they do not stop?
Click here to see answer by math_tutor2020(3816)  |
Question 1208250: The total distance of a family road trip is 668.25 miles. After traveling 50.75 miles, a kid asked how much longer it would take to get there. If the car travels 65 miles every hour, how many hours will it take to finish the trip, if they do not stop?
Click here to see answer by josgarithmetic(39617)  |
Question 1209277: A man makes a deposit of $50,000 into an account that pays an annual interest of 5%. How much money will be in the account after 10 years if:
I. The interest is compounded continuously
II. How long will it take for the money to triple itself if interest is compounded continuously?
Click here to see answer by math_tutor2020(3816)  |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160
|
| |


