SOLUTION: How many zeros are there at the end of 2005!

Algebra ->  Decimal-numbers -> SOLUTION: How many zeros are there at the end of 2005!      Log On


   

Question 945824: How many zeros are there at the end of 2005!
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
2005%21=1%2A2%2A3%2A4%2A5%2A%22....%22%2A2003%2A2004%2A2005
If there are n zeros at the end, it means that
2005%21=K%2A10%5En where K is an integer that is not divisible by 10
(it does not have any zeros at the end).

It all comes down to prime factorizations.
Since every even number
(from 2=1%2A2 to 2004=1002%2A2 ),
has 2 as a factor, I am sure that
the prime factorization of 2005%21=1%2A2%2A3%2A4%2A5%2A%22....%22%2A2003%2A2004%2A2005 includes 2 ,
repeated as a factor at least 1002 times.
I am sure that 5 must also appear as a factor many times
in the prime factorization of 2005%21=1%2A2%2A3%2A4%2A5%2A%22....%22%2A2003%2A2004%2A2005 ,
although not as many times as 2 does.
The 2's and 5's can be paired together
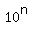to make 10=2%2A5 factors that together make the 10%5En part of 2005%21=K%2A10%5En .
Any leftover 2's will be part of K .
I am sure K has 2 repeated as a factor many times,
but it does not also have 5 as a factor,
so it is not a multiple of 10=2%2A5 .

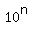
All the 5's that were factors of 2005%21=K%2A10%5En
are in 10%5En=%282%2A5%29%5En=2%5En%2A5%5En , and conversely,
all the n 5's that are factors of the 10%5En
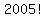were already in 2005%21=K%2A10%5En .

So, all we have to do is find the n exponent that 5 has in the prime factorization of 2005%21 .
Since 2005%2F5=401<--->2005=401%2A5 , we know that
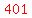5 appears at least red%28401%29 times in the prime factorization of 2005%21=1%2A2%2A3%2A4%2A5%2A%22....%22%2A2003%2A2004%2A2005 .
It appears in that factorial as the factor 5 ,
as the number 10=2%2A5, as the number 15=3%2A5 ,
and so on, all the way to the the factors
2000=400%2A5 and 2005=401%2A5 .
There are also some factors that contribute more than one 5 to the prime factorization.
For example, 25=5%2A5 and all its multiples
(such as 50 , 75 , 100 , 125 , and so on),
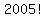contribute at least one extra 5 to the prime factorization of 2005%21 .
In all, 25 and its multiples contribute at least
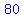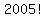blue%2880%29 extra 5's to the prime factorization of 2005%21 ,
because 2005%2F25=about80.2<--->80%2A25=2000%3C2005%3C81%2A25=2025 .
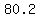Some of those multiples of 5 and 25 are also
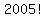
multiples of 125=5%5E3 , so they contribute to the prime factorization of 2005%21
one more 5 as a factor than the other multiples of 5 and 25 .
There are exactly green%2816%29 of those,
from 125=1%2A125 to 2000=16%2A125 because 16%3C2005%2F125=about16.04%3C17 .
Finally, among the numbers that are multiples of 5 , 25 and 125 , there are some
(like 625=5%5E4 and its multiples)
that contribute to the prime factorization of 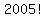2005%21
one more 5 as factor than all the others.
There are just red%283%29 of those:
625 , 1250=2%2A625 , and 1875=3%2A625 .

Taking into account
the 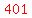red%28401%29 5's contributed by every multiple of 5 ,
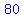the blue%2880%29 extra 5's contributed by every multiple of 25 ,
the green%2816%29 extra 5's contributed by every multiple of 125 , and
the red%283%29 extra 5's contributed by the multiples of 625 ,
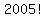there are exactly red%28401%29%2Bblue%2880%29%2Bgreen%2816%29%2Bred%283%29=highlight%28500%29 5's in the prime factorization of 2005%21 .