SOLUTION: Let a_n = 11...1 with 3^n digits. Prove that a_n is divisible by 3a_(n-1).

Algebra ->  Decimal-numbers -> SOLUTION: Let a_n = 11...1 with 3^n digits. Prove that a_n is divisible by 3a_(n-1).      Log On


   

Question 389515: Let a_n = 11...1 with 3^n digits. Prove that a_n is divisible by 3a_(n-1).
Found 2 solutions by richard1234, robertb:
Answer by richard1234(7193) About Me  (Show Source):
You can put this solution on YOUR website!
We have
a%5B0%5D+=+1
a%5B1%5D+=+111
a%5B2%5D+=+111111111, etc.

Proceed by induction. The base case n = 1 works, as 111 is divisible by 3.


For some k+%3E=+0,

a%5Bk%5D+=+%2810%5E%283%5Ek%29+-+1%29%2F9

Then, for k+1,

a%5Bk%2B1%5D+=+%2810%5E%283%5E%28k%2B1%29%29+-+1%29%2F9

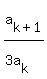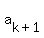It suffices to show that a%5Bk%2B1%5D%2F%283a%5Bk%5D%29 is an integer. Substituting a%5Bk%2B1%5D%7D%7D+and+%7B%7B%7Ba%5Bk%5D, we obtain:

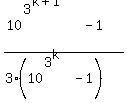
%2810%5E%283%5E%28k%2B1%29%29+-+1%29%2F%283%2A%2810%5E%283%5Ek%29-1%29%29

Letting z+=+10%5E%283%5Ek%29-1, we have



Rearrange the terms:



The last term is equivalent to the numerator in the fraction we wish to prove is an integer. Therefore, we can substitute this expression and obtain

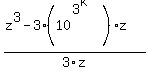%28z%5E3+-+3%2A%2810%5E%283%5Ek%29%29%2Az%29%2F3z (we are trying to prove this is an integer for all k)

Cancel out z from both sides to get

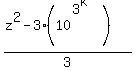
%28z%5E2+-+3%2A%2810%5E%283%5Ek%29%29%29%2F3

It now suffices to prove that the numerator is divisible by 3, which happens if and only if z%5E2 is divisible by 3. However, we already know that z+=+10%5E%283%5Ek%29+-+1 which is divisible by 3, since all powers of 10 are 1 modulo 3 (therefore subtracting 1 makes it 0 mod 3, i.e. divisible by 3). Hence, the expression is an integer, and we are done.

This is a somewhat lengthy proof, but rigorous proofs are sometimes more efficient and strong in terms of explaining their points. You'll definitely see proofs like this in contests like USAMO, IMO, and Putnam.

Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
a_1 = 111 = 111%2A10%5E0+=+111%2A%28%2810%5E3+-+1%29%2F%2810%5E3+-+1%29%29
a_2 = 111 111 111 =
a_3 = 111 111 111...111 (27 1's) =
........
a_n = by induction.
Then, substituting 999 for 10%5E3+-+1.


Now %2810%5E%282%2A3%5E%28n-1%29%29+%2B+10%5E%283%5E%28n-1%29%29+%2B+1%29%2F3 is definitely a positive integer, because the numerator is a positive integer with 2%2A3%5E%28n-1%29%2B1 digits, 2%2A3%5E%28n-1%29+-+2 of which are 0's, and 3 are 1's. Hence the sum of the digits of the numerator is 3, which makes the number itself divisible by 3.