SOLUTION: The sum of three numbers in a geometric progression GP is 13 and there products is -64. Find the numbers.

So, in standard designations, the terms are a, ar and ar^2.


From the problem, we have two equations

    a + ar + ar^2 =  13,     (1)   (the sum)

    a*(ar)*(ar^2) = -64.     (2)   (the product).


Equation (2) is the same as

    (ar)^3 = -64,

which gives us

    ar = -4.     (3)


We substitute ar = -4 into equation (1).  We get then

    a - 4 + ar^2 = 13,

    a + ar^2 = 13 + 4 = 17.    (4)


We also represent ar^2 as  (ar)*r = -4r.

Then equation (4) takes the form

    a - 4r = 17.    (5)


Now we have a system of two equations (3) and (5)

    ar = -4,        (3)

    a - 4r = 17.    (5)

    
From (3), express r = 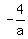  and substitute it into (5).  You will get

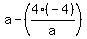     = 17,

     a^2 + 16 = 17a,

     a^2 - 17a + 16 = 0,

     (a-16)*(a-1) = 0.


It gives two possible solutions for 'a', 16 and 1.

    If a = 16,  then  r =  =  = .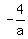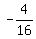

    If a =  1,  then  r = 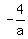 =  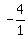=  -4.


Thus, two progressions are possible.


One progression is        16, -4, 1.                (*)

The other progression is   1, -4, 16   (the same as (*), but reversed)


Both progressions satisfy the imposed conditions.