|
Question 1208054: When expanded as a decimal, the fraction 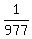 has a repetend (the repeating part of the decimal) that begins right after the decimal point, and is 976 digits long. If the last three digits of the repetend are ABC, compute the digits A, B, and C. has a repetend (the repeating part of the decimal) that begins right after the decimal point, and is 976 digits long. If the last three digits of the repetend are ABC, compute the digits A, B, and C.
A=
B=
C=
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(53475)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When expanded as a decimal, the fraction 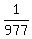 has a repetend (the repeating part of the decimal) has a repetend (the repeating part of the decimal)
that begins right after the decimal point, and is 976 digits long.
If the last three digits of the repetend are ABC, compute the digits A, B, and C.
A=
B=
C=
~~~~~~~~~~~~~~~~~
Let 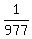 = x. Since the repetend is 977 digits long, we see that = x. Since the repetend is 977 digits long, we see that 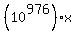 has the same decimal
expansion as x. Hence, the number n = has the same decimal
expansion as x. Hence, the number n = 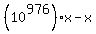 is an integer number and it is (it represents) the "repetend".
But, from the other side, this number n is
9999...999999
n = is an integer number and it is (it represents) the "repetend".
But, from the other side, this number n is
9999...999999
n = 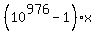 = --------------- .
977
+---------------------------------------------------------------+
| The numerator is the integer formed by 976 digits of "9". |
+---------------------------------------------------------------+
So, we can write 9999...999999 = 977*n, where n is some integer number. (1)
This number "n" is the "repetend part", and our goal is to find three last digits of n.
+-------------------------------------------------------------------+
| From this writing (1), it is clear that the last digit of n is 7, |
| providing 7*7 = 49 with the last digit 9; |
| so, we can write n = 10m+7 for some integer m. |
+-------------------------------------------------------------------+
Substitute it into (1). You will get
9999...999999 = 977*(10m+7) = 977*10m + 6839.
Hence, 9999...999999 = 977*10m + 6839. (2)
Subtract 6839 from both sides of (2). You will get
9999...9993160 = 977*10m (3)
In (3), divide both sides by 10. You will get
9999...999316 = 977*m, (4)
where the number in the left side has the last 3 digits 316 and all other preceding digits are "9", and "m" is some integer.
+-------------------------------------------------------------------+
| From this writing (4), it is clear that the last digit of m is 8, |
| providing 7*8 = 56 with the last digit 6; |
| so, we can write m = 10k+8 for some integer k. |
+-------------------------------------------------------------------+
Substitute it into (4). You will get
9999...999316 = 977*(10k+8) = 977*10k + 7816.
Hence, 9999...999316 = 977*10k + 7816. (5)
Subtract 7816 from both sides of (5). You will get
9999...991500 = 977*10k (6)
In (6), divide both sides by 10. You will get
9999...999150 = 977*k, (7)
where the number in the left side has the last 3 digits 134 and all other preceding digits are "9", and "k" is some integer.
+-------------------------------------------------------------------+
| From this writing (7), it is clear that the last digit of k is 0, |
| providing 7*0 = 0 with the last digit 0. |
+-------------------------------------------------------------------+
Thus the last three digits in repetend part are 087.
ANSWER. The last three digits in repetend part are 087.
So, A = 0, B = 8, C = 7. = --------------- .
977
+---------------------------------------------------------------+
| The numerator is the integer formed by 976 digits of "9". |
+---------------------------------------------------------------+
So, we can write 9999...999999 = 977*n, where n is some integer number. (1)
This number "n" is the "repetend part", and our goal is to find three last digits of n.
+-------------------------------------------------------------------+
| From this writing (1), it is clear that the last digit of n is 7, |
| providing 7*7 = 49 with the last digit 9; |
| so, we can write n = 10m+7 for some integer m. |
+-------------------------------------------------------------------+
Substitute it into (1). You will get
9999...999999 = 977*(10m+7) = 977*10m + 6839.
Hence, 9999...999999 = 977*10m + 6839. (2)
Subtract 6839 from both sides of (2). You will get
9999...9993160 = 977*10m (3)
In (3), divide both sides by 10. You will get
9999...999316 = 977*m, (4)
where the number in the left side has the last 3 digits 316 and all other preceding digits are "9", and "m" is some integer.
+-------------------------------------------------------------------+
| From this writing (4), it is clear that the last digit of m is 8, |
| providing 7*8 = 56 with the last digit 6; |
| so, we can write m = 10k+8 for some integer k. |
+-------------------------------------------------------------------+
Substitute it into (4). You will get
9999...999316 = 977*(10k+8) = 977*10k + 7816.
Hence, 9999...999316 = 977*10k + 7816. (5)
Subtract 7816 from both sides of (5). You will get
9999...991500 = 977*10k (6)
In (6), divide both sides by 10. You will get
9999...999150 = 977*k, (7)
where the number in the left side has the last 3 digits 134 and all other preceding digits are "9", and "k" is some integer.
+-------------------------------------------------------------------+
| From this writing (7), it is clear that the last digit of k is 0, |
| providing 7*0 = 0 with the last digit 0. |
+-------------------------------------------------------------------+
Thus the last three digits in repetend part are 087.
ANSWER. The last three digits in repetend part are 087.
So, A = 0, B = 8, C = 7.
Solved.
Answer by Edwin McCravy(20077)   (Show Source): (Show Source):
You can put this solution on YOUR website!
To get some insight as to what is going on here, I took
the long division out a few places, without skipping any
steps because of 0's, as we usually do in long division:
0.0 0 1 0 2
9 7 7)1.0 0 0 0 0
0
1 0
0
1 0 0
0
1 0 0 0
9 7 7
2 3 0
0
2 3 0 0
1 9 5 4
3 4 6
The very first remainder above is 1. The decimal will start repeating
when the remainder is 1 again, and the subtractions we perform to get a
remainder are always from a remainder that is annexed on the right with
a 0. So to get a 1 remainder, we must be subtracting a digit multiple
of 977 that ends in a 9.
The only digit multiple of 977 that ends with a 9 is 7x977 or
6839, so 1 more, or 6840 must have been the number we would be
subtracting 6839 from, which means the remainder just before the
remainder of 1 was 684. So the last digit before the digits started
repeating must have been a 7.
To have gotten the remainder 684 from a number that ended with 0, we
must have subtracted a digit multiple of 977 that ended with a 6.
The only digit multiple of 977 that ends with a 6 is 8x977 or
7816, so 684 more, or 8500 must have been the number we would be
subtracting 6839 from, which means the remainder just before the
remainder of 684 was 850. And the digit before the 7 must have
been an 8.
To have gotten the remainder 850 from a number that ended with 0, we
must have subtracted a digit multiple of 977 that ended with a 0,
which could only have been 0x977 or 0.
So the last three digits before we got a 1 remainder must have been 087
That's the answer 087. A=0, B=8, C=7
Edwin
|
|
|
| |