SOLUTION: Two gears rotate so that one completes 1 more revolution per minute than the other. If it takes the smaller gear 1 second less than the larger gear to complete 1/5 revolution, how

Answer.  Faster gear makes 4 revolutions per minute, while the slower gear makes 3 revolutions per minute.


Check.  The faster gear makes one revolution in 60/4 = 15 seconds.

        The slower gear makes one revolution in 60/3 = 20 seconds.


        Difference of times to make 1/5 revolution is  (20-15)/5 = 1 second.

Let n be the number of rotations of the faster gear per minute.

Then the number of rotations of the slower gear per minute is (n-1),  according to the condition.


The time to make one rotation for faster gear is 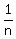   of an minute for the faster gear  and    of an minute for the slower gear.


The difference   - 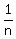  is equal to 5 seconds,  or    of the minute,  according to the condition.


So, the equation is


 -  = ,


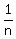and when you solve it, you will get the answer claimed above.