Question 1035337: Find the max/min point for the following function:
f (x,y) = x^3 + y^3 + 6xy
Answer by robertb(5830)   (Show Source):
You can put this solution on YOUR website!  and  .
Also,  and  , and 
Use the Second partial derivative test.
Set the partial derivatives above to 0 and solve for x and y.
 and  .
This system of equations yield two points as its solutions: (0,0) , (-2,-2). (Verify!!)
Now find the determinant of the hessian for each point.
For (0,0):  .
This implies that the point (0,0) is a saddle point (neither a local max nor a local min).
For (-2,-2):  .
Since 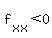 , it follows that (-2,-2) is a local maximum.
|
|
|
