Lesson Finding digits of the decimal expansion to the number 1/977

Algebra ->  Decimal-numbers -> Lesson Finding digits of the decimal expansion to the number 1/977      Log On


   

This Lesson (Finding digits of the decimal expansion to the number 1/977) was created by by ikleyn(52800) About Me : View Source, Show
About ikleyn:

Finding digits of the decimal expansion to the number 1/977


Problem 1

When expanded as a decimal,  the fraction 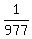  1%2F977  has a repetend  (the repeating part of the decimal)
that begins right after the decimal point,  and is  976  digits long.
If the last three digits of the repetend are  ABC,  compute the digits  A,  B,  and  C.

Solution 

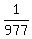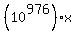Let 1%2F977 = x.  Since the repetend is 977 digits long, we see that  %2810%5E976%29%2Ax has the same decimal
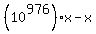expansion as x.  Hence, the number  n = %2810%5E976%29%2Ax-x  is an integer number and it is (it represents) the "repetend".

                                                                
But, from the other side,  this number  n  is  


                          9999...999999
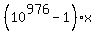    n = %2810%5E976-1%29%2Ax = --------------- .
                              977                                   


   +---------------------------------------------------------------+
   |    The numerator is the integer formed by 976 digits of "9".  |
   +---------------------------------------------------------------+


So, we can write  9999...999999 = 977*n, where n is some integer number.    (1)



This number "n" is the "repetend part",  and our goal is to find three last digits of n.



    +-------------------------------------------------------------------+
    | From this writing (1), it is clear that the last digit of n is 7, |
    |         providing 7*7 = 49 with the last digit 9;                 |
    |      so, we can write  n = 10m+7 for some integer m.              |
    +-------------------------------------------------------------------+


Substitute it into (1).  You will get


    9999...999999 = 977*(10m+7) = 977*10m + 6839.


Hence,  9999...999999 = 977*10m + 6839.    (2)


Subtract 6839 from both sides of (2).  You will get

        9999...9993160 = 977*10m           (3)


In (3),  divide both sides by 10.  You will get

        9999...999316 = 977*m,             (4)

where the number in the left side has the last 3 digits 316 and all other preceding digits are "9",  and "m" is some integer.


    +-------------------------------------------------------------------+
    | From this writing (4), it is clear that the last digit of m is 8, |
    |        providing 7*8 = 56 with the last digit 6;                  |
    |      so, we can write  m = 10k+8 for some integer k.              |
    +-------------------------------------------------------------------+



Substitute it into (4).  You will get


    9999...999316 = 977*(10k+8) = 977*10k + 7816.


Hence,  9999...999316 = 977*10k + 7816.    (5)


Subtract 7816 from both sides of (5).  You will get

        9999...991500 = 977*10k            (6)


In (6),  divide both sides by 10.  You will get

        9999...999150 = 977*k,             (7)

where the number in the left side has the last 3 digits 134 and all other preceding digits are "9",  and "k" is some integer.


    +-------------------------------------------------------------------+
    | From this writing (7), it is clear that the last digit of k is 0, |
    |        providing 7*0 = 0 with the last digit 0.                   |
    +-------------------------------------------------------------------+


Thus the last three digits in repetend part are  087.



ANSWER.  The last three digits in repetend part are  087.

         So,  A = 0,  B = 8,  C = 7.


This lesson has been accessed 613 times.