Question 845606: From a basket of mangoes, the King took 1/6, the Queen took 1/5 of the remainder, the three chief Princes to ¼, 1/3, and ½ of the successive remainders, respectively. The youngest child took the remaining 3 mangoes. How many mangoes were in the basket originally?
Found 2 solutions by ankor@dixie-net.com, KMST:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 

There is 5, 4, 3, and 2 in numerator and denominator.
They "cancel out" and you get
 so so  and and  . .
The interesting part is that the king took  of of  mangoes, mangoes,
which is  mangoes, mangoes,
and each person after the king took  mangoes too. mangoes too.
of the  mangoes left, the queen took mangoes left, the queen took
 mangoes, leaving mangoes, leaving
 . .
Then from those  the first prince took the first prince took  , ,
which was  mangoes, and so on. mangoes, and so on.
Each member of the family calculated his or her share very fairly.
Each one figured that the remaining mangoes were to be divided among the  family members that had not yet received a portion, and took the family members that had not yet received a portion, and took the 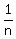 fair share, so they would all end up with the same amount. fair share, so they would all end up with the same amount.
|
|
|