Question 832321: The manager of a furniture factory finds that it costs $2,200 to manufacture 100 chairs in one day and $4,800 to produce 300 chairs in one day.
(a) assuming that relationship between cost and the number of chairs produced is linear, find an equation that express this relationship.
(b) what is the slope of the line in part (a) and what does it represent?
(c) what is the y- intercept of this line, and what does it represent?
Answer by math-vortex(648)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi, there--
THE PROBLEM:
The manager of a furniture factory finds that it costs $2,200 to manufacture 100 chairs in one day and $4,800 to produce 300 chairs in one day.
(a) Assuming that relationship between cost and the number of chairs produced is linear, find an equation that express this relationship.
(b) what is the slope of the line in part (a) and what does it represent?
(c) what is the y- intercept of this line, and what does it represent?
A SOLUTION:
(a) Assume that relationship between cost and the number of chairs produced is linear. Find an equation that express this relationship.
This sentence tells us to find an equation relating the cost to the number of chairs. Since the relationship is linear, this will be the equation for a line.
First choose variables. I like n and C because they remind me of number and cost, but we could choose any letters, x and y, whatever.
Let n be the number of chairs produced.
Let C be the cost (in dollars).
We need to determine which of these variable is independent and which in dependent. In this problem,
C is the dependent variable because the Cost varies depending upon how many chairs are produced. This
tells us the the horizontal axis is number of chairs produced n, and the vertical axis is the cost C.
In this problem we will follow the same process that we follow to come up with the equation for a line when we know two points. Don't let all the words here worry you too much.
First, we know that it costs $2,200 to produce 100 chairs. We can make an ordered pair out of this.
(n, C) = (100, 2200)
Second, we know that it costs $4800 to produce 300 chairs. The order pair for this data is
(n, C) = (300, 4800)
These points are on the line. We use them to find the slope m of the line. Remember that the slope is the
"rise over the run," or the vertical change divided by the horizontal change.
To find vertical change, we subtract "second C minus first C:" 4800-2200 = 2600. From the first data point to the second, the cost increased by $2,600.
To find the horizontal change, we subtract "second n minus first n:" 300-100 = 200. From the first data
point to the second, the number of chairs increased by 200.
The slope for our line is [vertical change] / [horizontal change] or
[change in Cost] / [change in number of chairs produced] = 2600/200
This is a fraction, so we can simplify it. Divided the numerator and denominator by 200
 The slope for the line is 13/1, or 13. Recall that the numerator in this fraction is Cost (in dollars), and the
denominator is the number of chairs produced. The slope tells that it costs $2600 to produced 200
chairs, but it also tells (after we reduced) that it costs $13 to produce 1 chair.
Now that we have the slope, we use one of our points and the slope to write an equation. The point-slope
form for a linear equation is
The slope for the line is 13/1, or 13. Recall that the numerator in this fraction is Cost (in dollars), and the
denominator is the number of chairs produced. The slope tells that it costs $2600 to produced 200
chairs, but it also tells (after we reduced) that it costs $13 to produce 1 chair.
Now that we have the slope, we use one of our points and the slope to write an equation. The point-slope
form for a linear equation is  where m is the slope and where m is the slope and 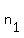 and and 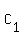 are values for a point on the line.
We will use qs for the slope and (100, 2200) for the point.
C - 2200 = 13(x - 100)
Simplify.
C - 2200 = 13x - 1300
C = 13x -1300 + 2200
C = 13x + 900
This is the equation that expresses the relationship between the number of chairs produced and the cost.
(b) What is the slope of the line in part (a) and what does it represent?
The slope of the line is 13 and it represents the COST PER CHAIR PRODUCED ($13 per chair).
(c) what is the y- intercept of this line, and what does it represent?
Recall that a y-intercept is the place when the line crosses the y-axis, where x = 0. In this problem, the
y-axis is the Cost axis, so
The y-intercept is the C-intercept, the C-vaue when n = 0. Substitute 0 for n in the equation.
C = 13n + 900
C = 13(0) + 900
C = 900
This is the cost to produce no chairs. It is often refried to as the start-up cost.
Look at the equation C = 13n + 900
It tells you that cost to produce n chairs is $900 to get started, plus $13 for each chair you produce.
Hope this helps! Feel free to email if you have any questions about the solution.
Good luck with your math,
Mrs. F
math.in.the.vortex@gmail.com are values for a point on the line.
We will use qs for the slope and (100, 2200) for the point.
C - 2200 = 13(x - 100)
Simplify.
C - 2200 = 13x - 1300
C = 13x -1300 + 2200
C = 13x + 900
This is the equation that expresses the relationship between the number of chairs produced and the cost.
(b) What is the slope of the line in part (a) and what does it represent?
The slope of the line is 13 and it represents the COST PER CHAIR PRODUCED ($13 per chair).
(c) what is the y- intercept of this line, and what does it represent?
Recall that a y-intercept is the place when the line crosses the y-axis, where x = 0. In this problem, the
y-axis is the Cost axis, so
The y-intercept is the C-intercept, the C-vaue when n = 0. Substitute 0 for n in the equation.
C = 13n + 900
C = 13(0) + 900
C = 900
This is the cost to produce no chairs. It is often refried to as the start-up cost.
Look at the equation C = 13n + 900
It tells you that cost to produce n chairs is $900 to get started, plus $13 for each chair you produce.
Hope this helps! Feel free to email if you have any questions about the solution.
Good luck with your math,
Mrs. F
math.in.the.vortex@gmail.com
|
|
|