Question 61205: Please reply ASAP!!!!Help me!!!!
Bob is traveling home at a constant speed. After one-half hour, he is 77.5 miles from home and after one hour, he is 55 miles from home. Write a linear equation that gives the distance from home,y (in miles), in terms of the time x (in hours). How long will it take Bob to get home?
Please answer this question AS SOON AS POSSIBLE!!!I'm REALLY CONFUSED AND FRUSTRATED WITH MY ALGEBRA HOMEWORK!!!!!!
Found 2 solutions by ankor@dixie-net.com, josmiceli:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Don't Panic, it's not that hard.
:
Bob is traveling home at a constant speed. After one-half hour, he is 77.5 miles from home and after one hour, he is 55 miles from home. Write a linear equation that gives the distance from home,y (in miles), in terms of the time x (in hours). How long will it take Bob to get home?
:
Think of it this way:
x1 = 1 (hrs); y1 = 55
x2 = .5; y2 = 77.5
:
From these coordinates he can find the slope: 
:
 = = 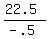 = -45 is our slope = -45 is our slope
:
Using the point slope formula: y - y1 = m(x - x1)
:
y - 55 = -45(x - 1)
y - 55 = -45x + 45
y = -45x + 45 + 55
y = -45x + 100 is our linear equation
:
When he's home the distance from home (y) = 0, find x
:
-45x + 100 = 0
-45x = -100
x = -100/-45
x = +2.22 hours to get home
:
Here is a qraph of the equation; x = number of hrs, y = distance from home.
:

:
Note all the information we can get from a simple equation derived from the
two points that they gave us: x1 = .5 hr, y1 = 77.5 mi & x2 = 1 hr; y2 = 55 mi
:
The slope is just the amount of change in y for a change in x. In our example
1 hour change has a 45 mi change in distance. The fact that it is -45 means that the distance is decreasing (getting closer to home and he is driving 45 mph)
:
Are you familiar with the y intercept? This occurs when x = 0, (the start of the journey). The graph crosses the y axis at y=100 (distance from home)
:
When the graph crosses the x axis, then y = 0, (at home now) and x = 2.2 hrs the time required to get home.
:
The fact that the graph is a straight line means he is driving the same speed thru out the journey.
:
As an example using the graph, how far is he from home after 3/4 hr? Would you say around 65 miles. We can find out exactly, of course, by using the equation and substituting .75 for x:
y = -45(3/4)- 100
y = -33.75 + 100
y = 66.25 miles from home is the actual miles
:
It's really quite wonderful how much information can be obtained from a simple linear equation and graph like. Hope this clarifies things for you
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! This problem requires careful reading.
Right away it says that Bob maintains the same speed. That
means he doesn't stop or slow down or speed up.
There's a stopwatch on him, and it says he traveled for .5 hour
and he was 77.5 miles from home. After 1 hour he was 55 miles
from home.
This is where you have to read carefully
after .5 hour he was 77.5 miles from home, and then, after
ANOTHER .5 hour he was 55 miles from home. So, during the 2nd
.5 hour, he covered 77.5 - 55 = 22.5 miles. That means his
rate of travel is 22.5 / .5 or 45 miles per hour.
D = total distance Bob traveled
x = time spent travelling
D = r*x
D = 45x
Now I ask, How long did it take Bob to travel the 77.5 miles to
home after he was on the road for .5 hr?
77.5 = 45x
x = 1.722 hours
That means it took Bob .5 + 1.722 = 2.222 hours to get home
You can figure it the other way, too.
After 1 hour, Bob was 55 miles from home. His time to cover
55 miles was
55 = 45x
x = 1.222 hours
That means he took 1 + 1.222 hours = 2.222 hours to get home
(agrees with my 1st result)
How many minutes is .222 hours?
.222*60 min/hr = 13.333 minutes
How many seconds is .333 minutes?
.333*60 sec/min = 20 seconds.
Bob took 2 hours 13 minutes and 20 seconds to get home
|
|
|