Question 224664: Working together, Joanne, Kent, and Geoff can process 504 orders per day for their business. Kent can process 20 more orders per day than Joanne can process. Geoff can process 104 fewer orders per day than Kent and Joanne combined. Find the number of orders that each person can process per day.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Write an equation for each statement:
:
"Working together, Joanne, Kent, and Geoff can process 504 orders per day for their business.":
j + k + g = 504
:
"Kent can process 20 more orders per day than Joanne can process."
k = j + 20
:
"Geoff can process 104 fewer orders per day than Kent and Joanne combined."
g = k + j - 104
we can also write it:
-j - k + g = -104
:
Find the number of orders that each person can process per day.
:
Add the 1st and above equation
j + k + g = 504
-j - k + g = -104
------------------ addition eliminate j and k, find g
2g = 400
g = 200 per day
:
Using the 1st equation, replace g with 200
j + k + 200 = 504
j + k = 504 - 200
j + k = 304
:
Rearrange the 2nd equation and add to the above equation
-j + k = 20
j + k = 304
---------------- additions eliminates j, find k
2k = 324
k = 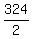
k = 162 per day
:
Find j using the 2nd equation, replace k with 162
162 = j + 20
162 -20 = j
j = 142 per day
:
our solutions: Joanne = 142, Kent = 162; Geoff = 200; (per day)
;
:
Check solution using the 1st statement
""Working together, Joanne, Kent, and Geoff can process 504 orders per day"
142 + 162 + 200 = 504
|
|
|