SOLUTION: find m and b in f(x)=mx+b such that f(2)=2 and f(-2)= -2. I am stumped!!!

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: find m and b in f(x)=mx+b such that f(2)=2 and f(-2)= -2. I am stumped!!!      Log On


   

Question 218283: find m and b in f(x)=mx+b such that f(2)=2 and f(-2)= -2.
I am stumped!!!
Answer by drj(1380) About Me  (Show Source):
You can put this solution on YOUR website!
Find m and b in f(x)=mx+b such that f(2)=2 and f(-2)= -2.

Step 1. We can interpret f(2)=2 as a point (2,2) and f(-2)=-2 as a point (-2,-2)

Step 2. The slope of the line m is given as

+m=%28y2-y1%29%2F%28x2-x1%29

where for our example is x1=-2, y1=-2, x2=2 and y2=2 (think of slope=rise%2Frun). You can choose the points the other way around but be consistent with the x and y coordinates. You will get the same result.

Step 3. Substituting the above values in the slope equation gives

m=%282-%28-2%29%29%2F%282-%28-2%29%29

m=4%2F4

m=1

Step 4. The slope is calculated as 1 or m=1

Step 5. Now use the slope equation of step 1 and choose one of the given points. I'll choose point (-2,-2). Letting y=y2 and x=x2 and substituting m=1 in the slope equation given as,

+m=%28y2-y1%29%2F%28x2-x1%29


+1=%28y-%28-2%29%29%2F%28x-%28-2%29%29

+1=%28y%2B2%29%2F%28x%2B2%29

Step 6. Multiply both sides of equation by x+2 to get rid of denomination found on the right side of the equation


+1%28x%2B2%29=%28x%2B2%29%28y%2B2%29%2F%28x%2B2%29


+1%28x%2B2%29=y%2B2


Step 7. Now simplify and put the above equation into slope-intercept form.

x%2B2=y%2B2

Subtract 2 from both sides of the equation

x%2B2-2=y%2B2-2

x=y

Step 8. See if the other point (2,2) or x=2 and y0intercept b=0 satisfies this equation

y=x

2=2 which is a true statement.

So the point (2,2) satisfies the equation and is on the line. In other words, you can use the other point to check your work.

Note; above equation can be also be transform into standard form as

-x%2By=0

See graph below to check the above steps.

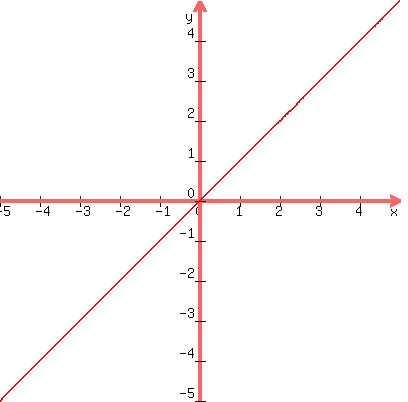
graph%28400%2C400%2C+-5%2C+5%2C+-5%2C+5%2C+x%29

Step 9. ANSWER: y=x is in slope-intercept form where m=1 and y-intercept b=0

I hope the above steps were helpful.

For FREE Step-By-Step videos in Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.

Good luck in your studies!

Respectfully,
Dr J