SOLUTION: HELP!!!! Ive been trying to solve this most irritating word problem and I cant manage to find the 3rd equation. The Problem is .... COFFEE. A coffee manufacturer sells a 10-pou

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: HELP!!!! Ive been trying to solve this most irritating word problem and I cant manage to find the 3rd equation. The Problem is .... COFFEE. A coffee manufacturer sells a 10-pou      Log On


   

Question 183069This question is from textbook Intermediate Algebra
: HELP!!!! Ive been trying to solve this most irritating word problem and I cant manage to find the 3rd equation. The Problem is ....
COFFEE. A coffee manufacturer sells a 10-pound package of coffee that consists of three flavors of coffee, vanilla flavored coffee costs $2/pound,Hazelnut costs $2.50/pound, and french roast cost $3/pound. The package contains the same amount of Hazelnut coffee as French roast coffee. The cost of the 10-pound package is $26. How many pounds of each type of coffee are in the package?

I labeled the equation as:
x- pounds of Vanilla flavored coffee
y- pounds of Hazelnut flavored coffee
z-pounds of French Roast flavored coffee
x + y + Z = 10
2x + 2.50y + 3z = $26
-Now if I can only manage to get the third variable Id be in good shape, BUT I just dont get it! What am I doing wrong??? This question is from textbook Intermediate Algebra

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Since the "package contains the same amount of Hazelnut coffee as French roast coffee", this means that y=z is your third equation. Since you have 3 equations in 3 unknowns, you can find a unique solution (if there is one) to the system.




Here's the Updated Solution:


x+%2B+y+%2B+z+=+10 Start with the first equation.


x+%2B+z+%2B+z+=+10 Plug in y=z. In other words, replace each "y" with "z"


x+%2B+2z+=+10 Combine like terms. Let's call this equation 4.


---------------------------------------------------


2x+%2B+2.50y+%2B+3z+=+26 Move onto the second equation


20x+%2B+25y+%2B+30z+=+260 Multiply EVERY term by 10 to make every number a whole number.


20x+%2B+25z+%2B+30z+=+260 Plug in y=z


20x+%2B+55z+=+260 Combine like terms. Let's call this equation 5.


-----------------------------------------------------------



So we have the system of equations 4 and 5:

system%28x%2B2z=10%2C20x%2B55z=260%29


Let's solve this smaller system by substitution


Now in order to solve this system by using substitution, we need to solve (or isolate) one variable. I'm going to solve for z.



So let's isolate z in the first equation


x%2B2z=10 Start with the first equation


2z=10-x Subtract x from both sides


2z=-x%2B10 Rearrange the equation


z=%28-x%2B10%29%2F%282%29 Divide both sides by 2


z=%28%28-1%29%2F%282%29%29x%2B%2810%29%2F%282%29 Break up the fraction


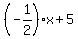z=%28-1%2F2%29x%2B5 Reduce



---------------------

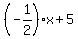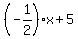
Since z=%28-1%2F2%29x%2B5, we can now replace each z in the second equation with %28-1%2F2%29x%2B5 to solve for x



20x%2B55highlight%28%28%28-1%2F2%29x%2B5%29%29=260 Plug in z=%28-1%2F2%29x%2B5 into the second equation. In other words, replace each z with %28-1%2F2%29x%2B5. Notice we've eliminated the z variables. So we now have a simple equation with one unknown.



20x%2B%2855%29%28-1%2F2%29x%2B%2855%29%285%29=260 Distribute 55 to %28-1%2F2%29x%2B5


20x-%2855%2F2%29x%2B275=260 Multiply


%282%29%2820x-%2855%2F2%29x%2B275%29=%282%29%28260%29 Multiply both sides by the LCM of 2. This will eliminate the fractions.


40x-55x%2B550=520 Distribute and multiply the LCM to each side



-15x%2B550=520 Combine like terms on the left side


-15x=520-550Subtract 550 from both sides


-15x=-30 Combine like terms on the right side


x=%28-30%29%2F%28-15%29 Divide both sides by -15 to isolate x



x=2 Divide



Since we know that x=2 we can plug it into the equation z=%28-1%2F2%29x%2B5 (remember we previously solved for z in the first equation).



z=%28-1%2F2%29x%2B5 Start with the equation where z was previously isolated.


z=%28-1%2F2%29%282%29%2B5 Plug in x=2


z=-2%2F2%2B5 Multiply


z=4 Combine like terms and reduce.




Now because we know that y=z and z=4, this tells us that y=4 also




========================= Answer =============================


So the solutions are

x=2, y=4 and z=4


which form the ordered triple (2,4,4)




This means that there are 2 lbs of Vanilla flavored coffee, 4 lbs of Hazelnut flavored coffee, and 4 lbs of French Roast flavored coffee