Question 1141303: A food factory is making a beverage for a customer from mixing two different existing products A and B. The compositions of A and B and prices ($/L) are given as follows,
Amount (L) in /100 L of A and B
Lime Orange Mango Cost ($/L)
A 3 6 4 8
B 8 4 6 7
The customer requires that there must be at least 4.5 Litres (L) Orange and at least 5 Litres of Mango concentrate per 100 Litres of the beverage respectively, but no more than 6 Litres of Lime concentrate per 100 Litres of beverage. The customer needs at least 70 Litres of the beverage per week.
a) Explain why a linear programming model would be suitable for this case study.
b) Formulate a Linear Programming (LP) model for the factory that minimises the total cost of producing the beverage while satisfying all constraints.
c) Use the graphical method to fi�nd the optimal solution. Show the feasible region and the optimal solution on the graph.What is the minimal cost for the product?
d)Is there a range for the cost ($) of A that can be changed without affecting the optimum solution obtained above?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! x = number of liters of product A.
y = number of liters of product B.
make a chart as shown below:
product A product B
lime per 100 liters 3 8
orange per 100 liters 6 4
mango per 100 liters 4 6
cost per liter 8 7
number of liters variable x y
your objective function is to minimize the cost.
the equation for that is cost = 8x + 7y
The customer requires that there must be at least 4.5 liters (L) Orange and at least 5 liters of Mango concentrate per 100 liters of the beverage respectively, but no more than 6 liters of Lime concentrate per 100 liters of beverage. The customer needs at least 70 liters of the beverage per week.
equation for at least 4.5 liters of orange is (6x + 4y)/100 >= 4.5
equation for at least 5 liters of mango is (4x + 6y)/100 >= 5
equation for not more than 6 liters of lime is (3x + 8y)/100 <= 6
equation for the customer needs at least 70 liters of the beverage every week is x + y >= 70
solve for y in each of these equations to get:
(6x + 4y)/100 >= 4.5 becomes y >= (450 - 6x) / 4
(4x + 6y)/100 >= 5 becomes y >= (500 - 4x) / 6
(3x + 8y)/100 <= 6 becomes y <= (600 - 3x) / 8
x + y >= 70 becomes y >= 70 - x
since the value of x and y can't be negative, then 2 more constraint equations are:
x >= 0
y >= 0
using the desmos.com calculator, you would then graph the OPPOSITE of these inequalities.
the area of the graph that is NOT shaded is your region of feasibility.
the corner points of this feasible region would then contain the least cost solution.
your constraint equations are:
(6x + 4y)/100 >= 4.5
(4x + 6y)/100 >= 5
(3x + 8y)/100 <= 6
x + y >= 70
x >= 0
y >= 0
the equations after you have solved for y become:
y >= (450 - 6x) / 4
y >= (500 - 4x) / 6
y <= (600 - 3x) / 8
y >= 70 - x
x >= 0
y >= 0
x >= 0 remains the same because there is no y in that equation to be solved for.
you will graph the opposite of these inequalities using the desmos.com calculator.
the equations to be graphed are:
y <= (450 - 6x) / 4
y <= (500 - 4x) / 6
y >= (600 - 3x) / 8
y <= 70 - x
x <= 0
y <= 0
your graph will look like this:
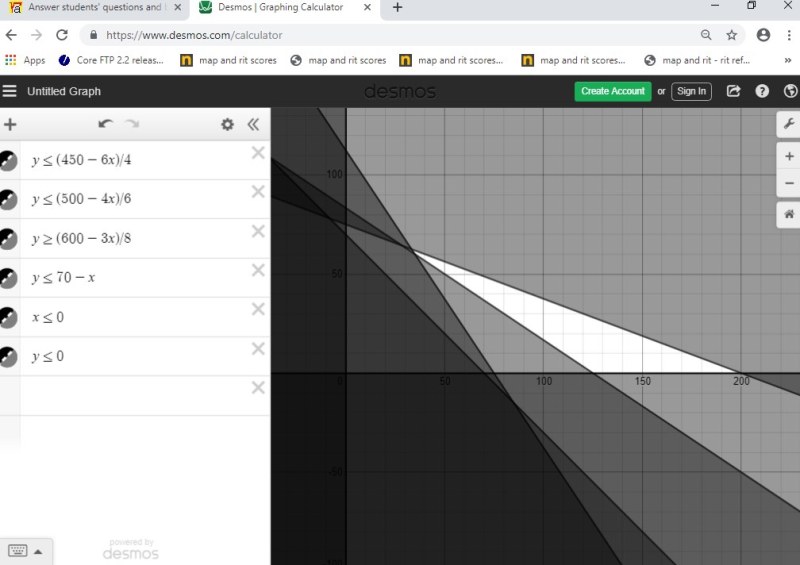
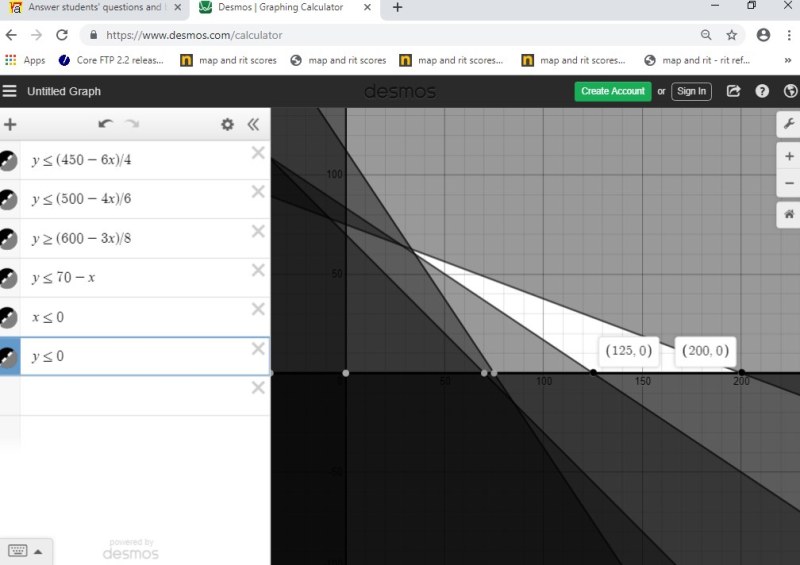
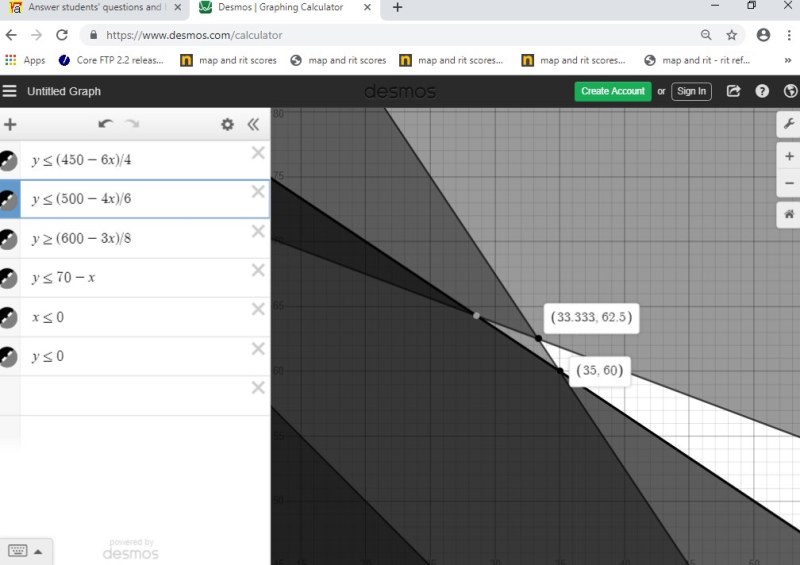
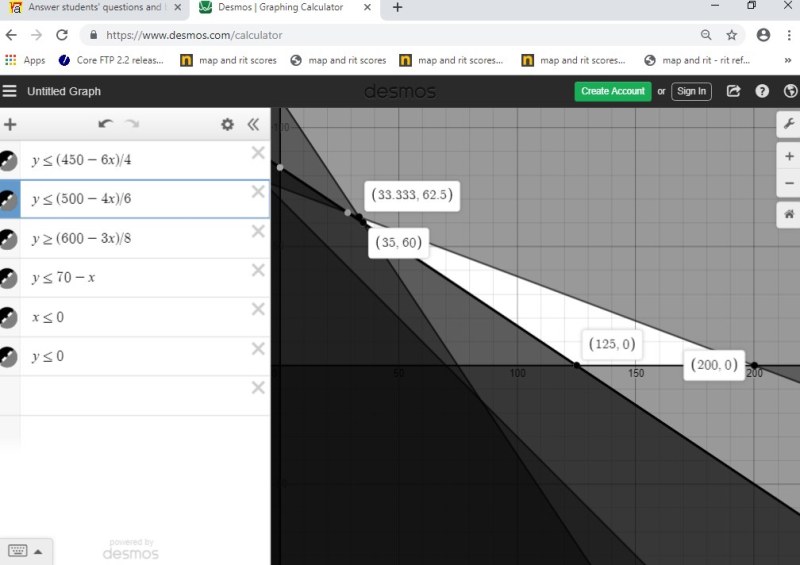
first graph is a full view without showing the corner points of the feasible region.
second graph is a full view showing two of the corner points of the feasible region.
third graph is a closeup view showing the other two corner points of the feasible region.
fourth graph is a full view showing all of the corner points of the feasible region.
the corner points of your feasible region are:
(33.333,62.5)
(35,60)
(125,0)
(200,0)
you evaluate the objective function at each of these corner points to get:
(33.333,62.5) yields a cost of 704.164
(35,60) yields a cost of 700
(125,0) yields a cost of 1000
(200,0) yields a cost of 1600
the lowest cost solution is the corner point of (35,60).
you would then evaluate that corner point to see if all the constraints have been met.
at the corner point of (35,60), .....
(6x + 4y)/100 >= 4.5 becomes (6*35 + 4*60)/100 >= 4.5 which becomes 4.5 >= 4.5 which is true.
(4x + 6y)/100 >= 5 becomes (4*35 + 6*60)/100 >= 5 which becomes 5 >= 5 which is true.
(3x + 8y)/100 <= 6 becomes (3*35 + 8*60)/100 <= 6 which becomes 4.5 <= 6 which is true.
x + y >= 70 becomes 35 + 60 >= 70 which becomes 95 >= 70 which is true.
x >= 0 and y >= 0 are both also true.
all constraint have been satisfied so the least cost solution is (35,60) which means that you would use 35 liters of solution A and 60 liters of solution B.
to find what cost for product A would make the least cost solution change hands, you would look at the two solutions that are closest to each other and see what cost of A would make the second lowest cost solution the least cost solution.
the second lowest cost solution will becomes the least cost solution when the following equation is satisfied.
note that some rounding in the second most least cost solution was used.
to make this as accurate as possible, that rounding needs to be removed.
the second least cost solution corner point on the graph is shown as (33.333,62.5).
that is really (100/3,62.5)
the second least cost is therefore really 100/3 * 8 + 62.5 * 7 = 704 and 1/6.
remove the mixed fraction and the second least cost is 4225/6.
so your least and next least cost equations and solutions are.
100/3 * 8 + 62.5 * 7 = 4225/6
35 * 8 + 60 * 7 = 700
you will be looking for the cost of product A, so make that cost equal to x rather than 8 to get the following equaitons.
100/3 * x + 62.5 * 7 = ???
35 * x + 60 * 7 = ???
the least cost solution will change hands when the second least cost solution becomes less than the least cost solution.
that will occur when 35 * x + 60 * 7 > 100/3 * x + 62.5 * 7
simplify that equation (it's really an inequality) to get:
35 * x + 420 > 100/3 * x + 437.5
multiply both sides of that inequality by 3 to get:
105 * x + 1260 > 100 * x + 1312.5
subtract 100 * x from both sides of that inequality and subtract 1260 from both sides of that inequality to get:
105 * x - 100 * x > 1312.5 - 1260
simplify to get 5 * x > 52.5
solve for x to get x > 10.5
when the cost for product A is greater than 10.5, the least cost solution will change hands with the next least cost solution.
for example, when x = 11, the cost at each corner point becomes:
(100/3,62.5) yields a cost of 100/3 * 11 + 62.5 * 7 = 804 and 1/6.
(35,60) yields a cost of 35 * 11 + 60 * 7 = 805
(125,0) yields a cost of 125 * 11 + 60 * 0 = 1375
(200,0) yields a cost of 200 * 11 + 60 * 0 = 2200
the lowest cost solution is now at (100/3,62.5) rather than at (35,60).
this can't be seen very easily graphically, but the following spreadsheet shows at what cost per liter for product A that the change over takes place.
one minimum cost is shown in red.
two equal minimum costs are shown in blue.

you can see from the spreadsheet that the minimum cost is at (35, 60) when the cost per liter for product A is less than 10.5.
when the cost per liter for product A is equal 10.5, then the minimum cost is shared between (35,60) and (33 and 1/3, 62.5).
when the cost per liter for product A is greater than 10.5, then the minimum cost is at (33 and 1/3, 62.5).
why was this problem suitable for a linear programming model?
from my perspective, there was an objective function which either had to be minimized or maximized, and they were constraints that had to be satisfied.
those were the two key factors that indicated to me that this was probably a linear programming type of problem.
|
|
|