Question 1120369: A rectangle has an area of 247 cm2 and a perimeter of 64 cm. What are its dimensions?
smaller side= ?cm
larger side= ?cm
Found 3 solutions by solver91311, greenestamps, ikleyn:
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are two basic approaches to this problem:
(1) let x be one dimension of the rectangle and use the given perimeter to find that (32-x) is the other dimension; then use the given area to write and solve the equation that says x times (32-x) is equal to 247.
or
(2) Find the two numbers whose product is equal to the given area of 247 and see if they give the correct perimeter of 64.
Note with the second option we are assuming that, since both the perimeter and area are whole numbers, the length and width of the rectangle are almost certain to be whole numbers.
So let's look at the first option, using formal algebra.
x(32-x) = 247
32x-x^2 = 247
x^2-32x+247 = 0
(x-?)(x-?) = 0
To finish the problem by this method, we are now faced with the task of finding two numbers whose product is 247 and whose sum is 32.
But that is exactly what we do with the second method!
So using formal algebra to solve the problem doesn't help get us any closer to the answer.
A bit if mental arithmetic finds that 247 = 13*19; and indeed the sum of 13 and 19 is 32.
So the dimensions of the rectangle are 13 and 19 cm.
Note an experienced problem solver might be clever in finding the two numbers whose product is 247 by noting that, since the sum of the two numbers is to be 32, the two numbers can be called 16+x and 16-x. That leads to...
(16+x)(16-x) = 247
256-x^2 = 247
x^2 = 9
x = 3 --> the two dimensions are 16+3=19 and 16-3=13.
Answer by ikleyn(52785)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I present here three major methods of solving this problem (and solving other problems of the same type).
1-st method
First method is to create a corresponding quadratic equation and then solve it using the quadratic formula.
Let x be the length of the rectangle, in centimeters, and
let y be its width.
Then 2x + 2y = 64.
Hence, 2y = 64 - 2x, and y =  = 32 - x.
The area of the rectangle is
x*y = x*(32-x) = - x^2 + 32x.
It is equal to 247 cm^2, which gives you an equation
-x^2 + 32x = 247, or
x^2 - 32x + 247 = 0. (1)
Apply the quadratic formula = 32 - x.
The area of the rectangle is
x*y = x*(32-x) = - x^2 + 32x.
It is equal to 247 cm^2, which gives you an equation
-x^2 + 32x = 247, or
x^2 - 32x + 247 = 0. (1)
Apply the quadratic formula
 = = 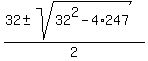 = = 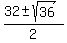 = = 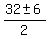 = = 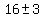 .
You have two roots: .
You have two roots:  = 16 + 3 = 19 and = 16 + 3 = 19 and  = 16 - 3 = 13.
Usually, the greater dimension is called the length.
So, in this problem the length is 19 centimeters.
Then the width is 32-19 = 13 centimeters.
Answer. The dimensions of the rectangle are 19 centimeters and 13 centimeters. = 16 - 3 = 13.
Usually, the greater dimension is called the length.
So, in this problem the length is 19 centimeters.
Then the width is 32-19 = 13 centimeters.
Answer. The dimensions of the rectangle are 19 centimeters and 13 centimeters.
Regarding this method, I'd like specially to highlight that the quadratic formula works for any quadratic equation.
It works like an army tank and provides a solution to any quadratic equation.
2-nd method
Second method is to create a correcponding quadratic equation and then solve it using factoring its left side.
Surely, the equation is the same as (1)
x^2 - 32x + 247 = 0, (1)
and the method of obtaining this equation remains the same as in the Solution 1.
Now we want to factor the left side in the form
(x - ?)*(x - ?) = 0. (2)
and now your goal is to find the numbers to put them instead of the question marks in order for to get the same equation (1).
It not very easy task. Your first wish is to try integer divisors of the number 247.
After some trials you will find them as 13 and 19.
Notice that their product is 13*19 = 247 and their sum is 13+19 = 32,
so (2) becomes equivalent to equation (1).
Now you get the same answer x= 19 as in the Solution 1.
Regarding this method, I'd like specially to highlight that it works good and fast when the coefficients of your original equation
are small and good enough to that extent that you can mentally find the required combination quickly.
Another situation when it works good is when you know the solution in advance.
3-rd method
It is most beatiful method.
You are given that the perimeter of the rectangle is 64 cm; hence, the sum of the length and the width is one half of that:
x + y = 32.
Then the average of the length and the width is one half of 32, i.e. 16.
It is clear that the values of x and y are remoted in the same value/distance "u" from 16, so we can write
x = 16 + u,
y = 16 - u.
Then the area is xy = (16+u)*(16-u) = 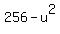 , and it is equal to 247, according to the condition.
Hence, , and it is equal to 247, according to the condition.
Hence, 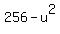 = 247, which gives = 247, which gives  = 256 - 247 = 9, and then u = = 256 - 247 = 9, and then u =  = 3.
Thus the length is x = 16 + u = 16 + 3 = 19,
and the width is x = 16 - u = 16 - 3 = 13.
We get the same answer quickly and mentally. = 3.
Thus the length is x = 16 + u = 16 + 3 = 19,
and the width is x = 16 - u = 16 - 3 = 13.
We get the same answer quickly and mentally.
You may find the third method in some recreational books.
Sometimes in math circles the teachers explain it to students.
In the school Math, the standard method of solution is to reduce the problem to a quadratic equation
and then solve it using the quadratic formula or factoring.
I presented the third method here to make your horizon wider.
If you demonstrate this method in the class, your teacher and your classmates will be impressed !
So, it was as if you visited a Math circle today . . .
==============
To see other solved similar problems using the third method, look into the lesson
- HOW TO solve the problem on quadratic equation mentally and avoid boring calculations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this textbook under the topic "Quadratic equations".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|