Question 1029850: A plain hamburger requires one ground beef patty and a bun. A cheeseburger requires one ground beef patty, one slice of cheese, and a bun. A double cheeseburger requires two ground beef patties, two slices of cheese, and a bun.
Frozen hamburger patties are typically sold in packs of 12; hamburger buns, in packs of 8; and cheese slices, in packs of 24.
A family is in charge of providing burgers for a neighborhood block party. They have purchased 14 packs of buns, 12 packs of hamburger patties, and 3 packs of cheese slices. How many of each type of sandwich should they make if they want to use up all of the buns, patties, and cheese slices?
plain hamburgers _____
cheeseburgers ______
double cheeseburgers ______
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! We start by giving variable names that will work as placeholders for the values we need to find:
 = number of plain burgers, = number of plain burgers,
 = number of cheeseburgers, = number of cheeseburgers,
 = number of double cheeseburgers. = number of double cheeseburgers.
(Some people like to use  , ,  , and , and 
but I like variable names that remind of their meaning).
All the burgers require  bun per burger, bun per burger,
so 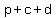 buns are needed, buns are needed,
and 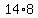 buns are available(14 packs of 8 buns per pack). buns are available(14 packs of 8 buns per pack).
That gives us the equation
 , or , or  . .
The plain burgers, and the cheeseburgers require one patty each,
but each double cheeseburger required 2 patties,
so the number of frozen hamburger patties required is
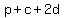 , ,
and 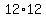 patties area available (12 packs, with 12 frozen hamburger patties per pack). patties area available (12 packs, with 12 frozen hamburger patties per pack).
That gives us the equation
 , or , or  . .
A plain hamburger requires no cheese,
while a cheeseburger requires one slice of cheese,
and a double cheeseburger required 2 slices,
so 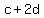 slices of cheese will be needed. slices of cheese will be needed.
There area 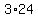 slices of cheese available (3 packs, with 24 slices per pack), slices of cheese available (3 packs, with 24 slices per pack),
and that gives us the equation
 or or  . .
The three equation form the easy system of linear equations
 . .
Subtracting the first equation from the second, we get
 . .
Substituting that value in the third equation we get
 --> -->  --> -->  --> -->  . .
Substituting the values found for  and and  into the first equation we get into the first equation we get
 --> -->  --> -->  --> -->  . .
plain hamburgers 72
cheeseburgers 8
double cheeseburgers 32.
|
|
|