The other tutor's proof is wrong. He proved the converse
of what you are to prove. He started by assuming
the conclusion and proved what was given. You must
start with what is given, not with what you are to
prove.
Here is the correct proof:
If b is a positive number and a < b
show that 

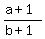
We start with what is given,
(not with what we are to prove, as he did):


 and use the hint:
and use the hint:
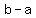

 We replace 0 by the equivalent ab - ab.
We replace 0 by the equivalent ab - ab.
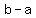

 We add ab to both sides:
We add ab to both sides:
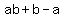

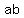 We add a to both sides
We add a to both sides
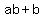

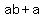 Factor out common factors on each side
Factor out common factors on each side
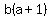

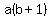 Divide both sides by b+1, which is positive
since b is positive. Therefore we will not
reverse the inequality when we divide by b+1:
Divide both sides by b+1, which is positive
since b is positive. Therefore we will not
reverse the inequality when we divide by b+1:


 Divide both sides by b which is positive and
also will not reverse the inequality when we
divide by it:
Divide both sides by b which is positive and
also will not reverse the inequality when we
divide by it:
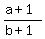

 which is equivalent to
which is equivalent to


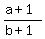 Edwin
Edwin