Question 1012279: There are 20 true/false questions and 20 multiple choice questions on a test.
A correct answer to a true false question earns 10 points.
A correct answer to a multiple choice question earns 12 points.
The test makers determined that it takes, on average, 3 minutes to answer a true/false question and 4 minutes to answer a multiple choice question. Students have 1 hour to answer to answer at most 18 questions of their choice. How many of each kind of question should a student answer correctly to get the greatest possible score?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website!  = number of true/false questions answered
 = number of multiple choice questions answered
Since "A correct answer to a true false question earns 10 points" and
"A correct answer to a multiple choice question earns 12 points",
 , which is a linear function on two variables.
We have some constraints that limit the domain of that function.
 and  are implicit constraints.
"Students have ... to answer to answer at most 18 questions of their choice",
 ,
is an explicit constraint that sounds strange to a rat-race accustomed American,
who would expect that instead students would be required to rush to answer as many questions as possible,
and maybe to answer a minimum number of questions, as in  .
Maybe the students are only given credit for  questions in order to encourage them to take time and work carefully, instead of rushing to answer as many questions as possible.
The expected pace, "it takes, on average, 3 minutes to answer a true/false question and 4 minutes to answer a multiple choice question", means that
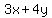 = time (in minutes) needed to answer true/false questions and multiple choice questions.
That leads to another explicit constraint of the problem, because the student can use at most  minutes (1 hour).
That constraint can be written as
 .
The line  obviously passes through  and  , so we graph it as  , and since  is a solution to ,
the graph for ,  , includes the origin, the point (0,0) .
Working in the same manner, we find that the constraint can be graphed as  ,
while would be graphed as  .
With the constraints  , we have four inequalities that determine a feasibility space that is a convex polygon. It is
 , with vertices at (0,0) , (0,15) , (12,6) , and (18,0) .
An extreme value (maximum or minimum) of linear function, such as , defined on a domain that is a ,
occurs at a vertex of the domain, or all along an edge between two vertices,
so we only need to check the scores for the vertices.
At (0,0) , obviously  .
At (0,15) ,  , and  .
At (18,0) ,  , and  .
At (12,6) ,  ,  , and the student gets the greatest possible score.
|
|
|
