SOLUTION: 8 womens and 12 girls can paint a large mural in 10 hours. 6 womens and 8 girls can paint the same mural in 14 hours. How long it would take to paint the mural one women? How long

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: 8 womens and 12 girls can paint a large mural in 10 hours. 6 womens and 8 girls can paint the same mural in 14 hours. How long it would take to paint the mural one women? How long       Log On


   

Question 1005375: 8 womens and 12 girls can paint a large mural in 10 hours. 6 womens and 8 girls can paint the same mural in 14 hours. How long it would take to paint the mural one women? How long it would take to paint the mural one girl?
* The answer has to be linear equation: reduction, equalization or replacement.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
The problem description is Uniform Rates for Work or Job.
RT=J relates work rate, time, amount or number of jobs.
The meaning of 1 job is "painting one mural".

Each agent doing work is imagined to work at a constant rate, and this rate is the same for each agent doing the work. If one agent works at rate R, then n agents working together do so at n*R.

Assign Variables:
system%28R=rateForOneWoman%2Cr=rateForOneGirl%29


Transcribe the description into a system of equations:
system%28%288R%2B12r%29%2A10=1%2C%286R%2B8r%29%2A14=1%29
This is a system of two linear equations in the variables, R and r. You can choose substitution method or elimination method, depending on what instructions you have.

Simplify the system first.
system%2880R%2B120r=1%2C84R%2B112r=1%29

80R=1-120r
R=%281-120r%29%2F80----this can be used again later.
-
84%281-120r%29%2F80%2B112r=1, making the substitution
84%281-120r%29%2B80%2A112r=80
84-10080r%2B8960r=80
84=80%2B%2810080-8960%29r
84=80%2B1120r
4=1120r
1=280r
highlight%28r=1%2F280%29------ONE mural in 280 HOURS, the one-girl rate.

Find the one-woman rate using the value for r.
R=%281-120%281%2F280%29%29%2F80
R=%281-12%2F28%29%2F80
R=%281-3%2F7%29%2F80
R=%284%2F7%29%2F80
R=4%2F560
highlight%28R=1%2F140%29--------One-woman rate is 140 hours to paint one mural.


You could also setup the problem using variables for TIME for each type of person to paint 1 mural, so g for girl, w for woman, those variables being TIME in HOURS, the rates for them would be 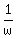1%2Fg and 1%2Fw.

Answer by ikleyn(52798) About Me  (Show Source):
You can put this solution on YOUR website!
.
8 highlight%28women%29 and 12 girls can paint a large mural in 10 hours. 6 highlight%28women%29 and 8 girls can paint the same mural in 14 hours.
How long it would take to paint the mural one highlight%28woman%29? How long it would take to paint the mural one girl?
* The answer has to be linear equation: reduction, equalization or replacement.
---------------------------------------------------------------------------- 
Let w = number of hours it would take to paint the mural one woman.
Let g = number of hours it would take to paint the mural one girl.

Then one woman paints 1%2Fw of the mural per hour. 8 women paint 8%2Fw of the mural per one hour.
One girl paints 1%2Fg of the mural per hour. 12 girls paint 12%2Fg of the mural per one hour.

In this way you get the system of two equations 

8%2Fw + 12%2Fg = 1%2F10,   (1)

6%2Fw + 8%2Fg = 1%2F14.    (2)

for two unknowns w and g. To solve it, multiply equation (1) by 2 (both sides) and equation (2) by -3, then add.
Thus you exclude the variable g and get an equation for the variable w only:

16%2Fw+-+18%2Fw = 2%2F10+-+3%2F14,   or

-2%2Fw = 14%2F70+-+15%2F70 = -1%2F70.

It gives w = 140. Hence, it takes 140 hours for 1 woman to paint the mural.

Now please complete the solution yourself.