Question 434087: solve this equation by sustitution
x=8-4y
2x-3y=13
Found 3 solutions by mananth, ikleyn, josgarithmetic:
Answer by mananth(16949)   (Show Source):
You can put this solution on YOUR website! 2x-3y = 13 .............1
4y=8-x ---------2
/4
y=2-0.25x
Plug the value of y in (1)
2x-3(2-0.25x)=13
2x-6+0.75x=13
2x+0.75 x=13+6
2.75 x = 19
/ 2.75
x= 6.91
Plug the value of x in (1)
2x-3y=13
2*6.91-3y=13
13.82 -3y=13
-3y=-0.82
/-3
y=0.27
Answer by ikleyn(53538)  (Show Source):
You can put this solution on YOUR website! .
solve this equation by  substitution
x=8-4y
2x-3y=13
~~~~~~~~~~~~~~~~
The way, which @mananth took for the solution in his post, I would compare with a driver,
who chooses to drive off-road parallel to a highway, instead of driving on the paved highway.
In this problem, you are very lucky, because one equation (first one of the two)
is just presented in the form ready for substitution.
So, use this (first) equation and replace 'x' in the second equation by 8-4y.
You will get then
2(8-4y) - 3y = 13.
Thus you have single equation for one unknown 'y', and you can easy solve it
16 - 8y - 3y = 13,
16 - 11y = 13,
16 - 13 = 11y,
3 = 11y,
y =  .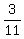
Having 'y', substitute this value into the first equation and find 'x'
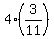x = 8 -  = 8 -  =  =  .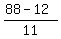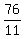
ANSWER. x = 76/11; y = 3/11.
Solved. The EXACT solution is obtained in rational numbers,
in opposite to the approximate answer in the post by @mananth, expressed in decimals.
------------------------
It is good to use decimals when it is needed.
But it is not good using decimals when it is not needed.
If to consider the solution by @mananth as a way and a tool for teaching students,
I would say that this way and this solution are inappropriate.
Not because I want to look very smart, but because what I said is a fact.
Answer by josgarithmetic(39713)  (Show Source):
|
|
|
