Question 389518: how to solve (-10,-5) and (-8,-2) with the equation y-y1=m(x-x1)
Found 2 solutions by haileytucki, MathTherapy:
Answer by haileytucki(390)   (Show Source):
You can put this solution on YOUR website! (-10,-5),(-8,-2)
Slope is equal to the change in y over the change in x, or 'rise over run'.
m=(change in y)/(change in x)
The change in x is equal to the difference in x-coordinates (also called run), and the change in y is equal to the difference in y-coordinates (also called rise).
m=(y2-y1)/(x2-x1)
Substitute in the values of x and y into the equation to find the slope.
m=(-2-(-5))/(-8-(-10))
Multiply -1 by each term inside the parentheses.
m=(-2-(-5))/(-8+10)
Add 10 to -8 to get 2.
m=(-2-(-5))/(2)
Multiply -1 by each term inside the parentheses.
m=(-2+5)/(2)
Add 5 to -2 to get 3.
m=(3)/(2)
After finding the slope between the points, use point-slope form to setup the equation. Point-slope is derived from the equation for slope m=((y2-y1))/((x2-x1)).
(y-(-5))=(3)/(2)*(x-(-10))
Remove the parentheses around the expression y-(-5).
y-(-5)=(3)/(2)*(x-(-10))
Multiply -1 by each term inside the parentheses.
y-(-5)=(3(x+10))/(2)
Multiply -1 by each term inside the parentheses.
y+5=(3(x+10))/(2)
Since 5 does not contain the variable to solve for, move it to the right-hand side of the equation by subtracting 5 from both sides.
y=-5+(3(x+10))/(2)
Simplify the right-hand side of the equation.
y=(3x+20)/(2)
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! how to solve (-10,-5) and (-8,-2) with the equation y-y1=m(x-x1)
Obviously, you need to create, not solve an equation in y = mx + b format, using the coordinates (-10, - 5) and (-8, - 2).
Find the slope or m:  ......  ...... ......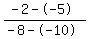
With m, or slope = and one coordinate point (-8, - 2), we can use the point-slope formula to determine the linear equation:  __ __ __ __
|
|
|
