First we look at the first equation:
The slope is -2 which has a 1 denominator 
The y-intercept is 9. So we start at 9 on the y-axis
and go down 2 units (since it's negative) and go right 1 unit,
like this:
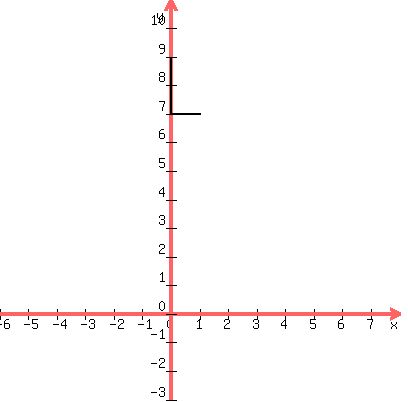Then we take a ruler and draw a straight line through where
we started and where we ended, like this:
Now we look at the second line,
The slope is 
. The y-intercept is 2. So we start at 2
on the y-axis and go up 1 unit (since it's positive) and go right
3 units, like this:
[Wow! that pokes right in to the other line!] Then we take the
ruler and draw a straight line through where we started and where
we ended, like this:
Now we can tell where they cross. Right there where that poked
into the first line. If you draw a line straight down to the
x-axis, you see that the x-coordinate is 3.
There's already a line straight over the the y-axis, so you can
now see that the y-coordinate is also 3. That means that the
solution is (x,y) = (3,3).
We can now check to make sure it's correct by substituting x=3 and
y=3 in both original equations:
So it checks.
Edwin
