Question 978141: the line y=2x+7 is parallel to the line y=2x-3.The line y= -0.5x+7 is perpendicular to the line y=2x-3. Find the perpendicular distance between the pair of parallel lines.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Line  is parallel to line is parallel to line  , ,
which is perpendicular to  , ,
so  and and  are perpendicular to each other. are perpendicular to each other.
So the distance between  and and 
is the distance, along  , ,
between the points where  intersects the other two lines. intersects the other two lines.
Lines  and and  obviously intersect at point obviously intersect at point 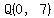 , the y-intercept for both lines. , the y-intercept for both lines.
We can find the point  where where  and and  intersect intersect
by solving 
I wanted to graph anyway, and in the graph it looked like it was 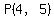 . .
Substituting  to see that to see that  for both lines confirmed that solution: for both lines confirmed that solution:
 and and 

The distance from 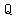 and and 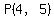
is the distance between  and and  . .
The distance between two points can be calculated according to a formula:
 , ,
but there is no need (usually) to memorize formulas,
if you understand their meaning.
That distance is the hypotenuse of a right triangle,
like the one in my drawing,
whose legs, parallel to the x-axis and y-axis,
are the horizontal distance and the vertical distance between the points.
In this case,
 (rounded). (rounded).
|
|
|