Question 923081: solve this problem using elimination substitution and graphing
1)p+3q=16
p+q=6
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Elimination/Addition
 .......eq.1 .......eq.1
 .........eq.2 .........eq.2
____________subtract 2 from 1





go to  .........eq.2, plug in .........eq.2, plug in  for for 



by SUBSTITUTION
 .......eq.1 .......eq.1
 .........eq.2 .........eq.2
____________
 .......eq.1..solve for .......eq.1..solve for 
 ...substitute in 2 ...substitute in 2
 .........eq.2..solve for .........eq.2..solve for 

 ...both sides multiply by ...both sides multiply by 

 ....substitute in eq.1 ....substitute in eq.1
 .......eq.1 .......eq.1



by Graphing
In order to graph these equations, we need to solve for q for each equation.
 .......eq.1 .......eq.1
 .........eq.2 .........eq.2
____________
 .......eq.1 .......eq.1
 .........eq.2 .........eq.2
____________
 .......eq.1 .......eq.1
 .........eq.2 .........eq.2
____________
now find two points that lie on each line
 .......eq.1...set .......eq.1...set 
 ...solve for ...solve for 

 ...if denominator same, numerator must be same too ...if denominator same, numerator must be same too

point is ( , , )=> x(or p)-intercept )=> x(or p)-intercept
 .......eq.1...set .......eq.1...set 
 ...solve for ...solve for 

point is ( , ,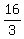 )=> y(or q)-intercept )=> y(or q)-intercept
 .........eq.2 .........eq.2
 .......eq.2...set .......eq.2...set 
 ...solve for ...solve for 

point is ( , , )=> x(or p)-intercept )=> x(or p)-intercept
 .......eq.2...set .......eq.2...set 
 ...solve for ...solve for 

point is ( , , )=> y(or q)-intercept )=> y(or q)-intercept
plot points ( , , ) and ( ) and ( , ,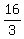 ) and draw a line ) and draw a line 
plot points ( , , ) and ( ) and ( , , )and draw a line )and draw a line 

|
|
|