Question 888794: Solve the following system graphically
4y = x + 4
x = 2/3y + 8/3
Answer by algebrapro18(249)   (Show Source):
You can put this solution on YOUR website! Steps for solving a system of equation graphically:
1)Get the first equation into y=mx+b form(solve for y)
2)Find your M and B(M=slope and B = Y-intercept)
3)Use your B and M to find two points on the line. These points will be (0,B) and (0+Change in x,B+Change in y).
4)Get the second equation into y=mx+b form(solve for y)
5)Find your M and B(M=slope and B = Y-intercept)
6)Use your B and M to find two points on the line. These points will be (0,B) and (0+Change in x,B+Change in y).
7)Graph the lines(plot the points from 3 and connect them and plot the points from 6 and connect them)
8) Find the point where the two lines intersect.
These will be the steps you follow for every problem you need to solve systems graphically.
For our problem we:
1) Solve 4y=x+4 for y
4y=x+4 divide both sides by 4
y = 1/4x + 1
2) Our m = 1/4 and our b = 1. Remember that slope is change in y over change in x we will need that for the next step.
3)Our points are going to be (0,b) and (0+Change in x,B+Change in y). Plugging in we get (0,1) and (0+4,1+1) or (4,2).
4) Solve 2/3y+8/3 = x for y
 subtract 8/3 from both sides
 Multiply both sides by 3/2
y =  =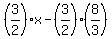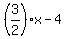 
5) Our m = 3/2 and our b = -4.
6)Our points are going to be (0,-4) and (0+2,-4+3) or (2,-1).
I will leave you to graphing the points (0,1),(4,2),(0,-4), and (2,-1) and seeing where the two lines intersect but you should get the point (4,2).
|
|
|
