2x - y + 2z = -8
-x + 3y - 4z = 15
x + 2y - 3z = 9
[ 2 -1 2 | -8]
[-1 3 -4 | 15]
[ 1 2 -3 | 9]
Get a zero where the -1 is on the 2nd row is by
multiplying the first row by 1 and adding it
to 2 times the second row:
1[ 2 -1 2 | -8]
2[-1 3 -4 | 15]
[ 1 2 -3 | 9]
[ 2 -1 2 | -8]
[ 0 5 -6 | 22]
[ 1 2 -3 | 9]
Get a zero where the 1 is on the 3rd row is by
multiplying the first row by 1 and adding it
to -2 times the third row:
1[ 2 -1 2 | -8]
[ 0 5 -6 | 22]
-2[ 1 2 -3 | 9]
[ 2 -1 2 | -8]
[ 0 5 -6 | 22]
[ 0 -5 8 |-26]
Get a 0 where the -5 is on the third row by
multiplying the second row by 1 and adding it
to 1 times row 3:
[ 2 -1 2 | -8]
1[ 0 5 -6 | 22]
1[ 0 -5 8 |-26]
[ 2 -1 2 | -8]
[ 0 5 -6 | 22]
[ 0 0 2 | -4]
-1,2,-2
Get a 1 where the 2 is in the first row by
dividing the first row through by 2
Get a 1 where the 5 is in the second row by
dividing the second row through by 5
Get a 1 where the 2 is in the third row by
dividing the third row through by 2
[ 1 
1 | -4]
[ 0 1 
| 
]
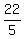[ 0 0 1 | -2]
Convert back to three equations:
= 
=
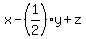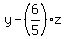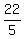
Substitute z = -2 into the second equation
=
=
= 
= 
= 
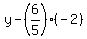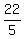
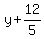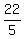
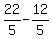
Finally substitute 
and 
into the first equation:
=
=
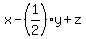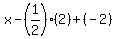So the solution is
(x, y, z) = (-1, 2, -2)
Edwin
(